nierówność Wiesiu: |16x²−4|<4 jak to prawidłowo obliczyć?

Wiesiu: 16x²−4<4 wyszło mi x∊(−√2/2,√2/2)

Wiesiu: 16x²−4>−4

Wiesiu: wychodzi chyba tylko 0

Bogdan: Rozwiąż nierówność podwójną: −4 < 4(4x² − 1) < 4 przedtem dzieląc ją obustronnie przez 4.

Wiesiu: wartość bez. nie może być ujemna,

Wiesiu: czyli ten drugi odpada?

Wiesiu: sorry, nie ten film

Wiesiu: dziękuje

Bogdan: Na wszelki wypadek pokaże pełne rozwiązanie.

	2
−4 < 4(4x2 − 1) < 4 ⇒ −1 < 4x2 − 1 < 1 ⇒ 0 < 4x2 < 2 ⇒ 0 < x2 <
	4

	2		√2		√2
x2 > 0 i x2 −		< 0 ⇒ x ≠ 0 i (x −		)(x +		) < 0
	4		2		2

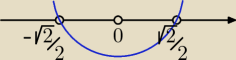
	−√2		√2
Odp.: x ∊ (		, 0)∪(0,		)
	2		2

Liczba 0 nie wchodzi do zbioru rozwiązań, |16*0² − 4| = |−4| = 4, a nie < 4

alinka: 1. Rozwiąż równość 16x²−4= 0 x1=1/2 x2=−1/2 2. Rozwiązujemy zadanie w przedziałach: a/ X∊(−∞,−1/2) b/ x∊(1/2, +∞) − wyrażenie w nawiasie zawsze jest nieujemne, czyli /16x²−4/<4 ad. a/ b/ 16x² − 4 − 4 = 0 16x²−8=0 2x²−1=0 x=+/− sqrt((1/2)

Bogdan:

	1
alinko, rozwiązaniem jest przedział. Twoje rozwiązania: x = ±		nie spełniają
	√2

zadanej nierówności.

	1
|16* (±		)2 − 4| < 4 ⇒ |8 − 4| < 4 ⇒ |4| < 4 sprzeczność
	√2