Janek191:
3
4x = t > 0
3
12x − 11*3
8x + 19*3
4x − 9 ≥ 0
( 3
4x)
3 − 11*( 3
4x)
2 + 19*3
4x − 9 ≥ 0
t
3 − 11 t
2 + 19 t − 9 ≥ 0
t = 1 jest pierwiastkiem równania t
3 − 11 t
2 + 19 t − 9 = 0
Wykonuję dzielenie:
( t
3 − 11 t
2 + 19 t − 9 ) : ( t − 1 ) = t
2 − 10 t + 9
−t
3 + t
2
−−−−−−−−
− 10 t
2 + 19 t
10 t
2 − 10 t
−−−−−−−−−−−−−
9 t − 9
− 9t + 9
−−−−−−
0
oraz t
2 − 10 t + 9 = ( t − 1)*( t − 9)
Mamy więc nierówność
(t − 1)*( t − 1)*( t − 9) ≥ 0
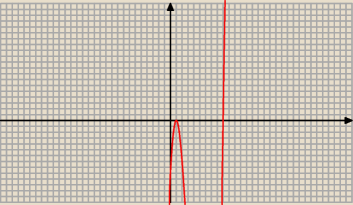
Rysujemy wykres i odczytujemy rozwiązania:
t ∊ < 9 ; +
∞ ) ∪ { 1 }
więc
3
4x = 1 lub 3
4x ≥ 9
4x = 0 lub 3
4x ≥ 3
2
x = 0 lub 4x ≥ 2
x = 0 lub x ≥ 0,5
=======================
 34x = t > 0
312x − 11*38x + 19*34x − 9 ≥ 0
( 34x)3 − 11*( 34x)2 + 19*34x − 9 ≥ 0
t3 − 11 t2 + 19 t − 9 ≥ 0
t = 1 jest pierwiastkiem równania t3 − 11 t2 + 19 t − 9 = 0
Wykonuję dzielenie:
( t3 − 11 t2 + 19 t − 9 ) : ( t − 1 ) = t2 − 10 t + 9
−t3 + t2
−−−−−−−−
− 10 t2 + 19 t
10 t2 − 10 t
−−−−−−−−−−−−−
9 t − 9
− 9t + 9
−−−−−−
0
oraz t2 − 10 t + 9 = ( t − 1)*( t − 9)
Mamy więc nierówność
(t − 1)*( t − 1)*( t − 9) ≥ 0
Rysujemy wykres i odczytujemy rozwiązania:
t ∊ < 9 ; + ∞ ) ∪ { 1 }
więc
34x = 1 lub 34x ≥ 9
4x = 0 lub 34x ≥ 32
x = 0 lub 4x ≥ 2
x = 0 lub x ≥ 0,5
=======================
34x = t > 0
312x − 11*38x + 19*34x − 9 ≥ 0
( 34x)3 − 11*( 34x)2 + 19*34x − 9 ≥ 0
t3 − 11 t2 + 19 t − 9 ≥ 0
t = 1 jest pierwiastkiem równania t3 − 11 t2 + 19 t − 9 = 0
Wykonuję dzielenie:
( t3 − 11 t2 + 19 t − 9 ) : ( t − 1 ) = t2 − 10 t + 9
−t3 + t2
−−−−−−−−
− 10 t2 + 19 t
10 t2 − 10 t
−−−−−−−−−−−−−
9 t − 9
− 9t + 9
−−−−−−
0
oraz t2 − 10 t + 9 = ( t − 1)*( t − 9)
Mamy więc nierówność
(t − 1)*( t − 1)*( t − 9) ≥ 0
Rysujemy wykres i odczytujemy rozwiązania:
t ∊ < 9 ; + ∞ ) ∪ { 1 }
więc
34x = 1 lub 34x ≥ 9
4x = 0 lub 34x ≥ 32
x = 0 lub 4x ≥ 2
x = 0 lub x ≥ 0,5
=======================
