.. Piotr 10: Funkcja f określona jest wzorem f(x)=√6+x−2x². Wyznacz: a) dziedzinę funkcji f ; b) najmniejsza oraz największą wartość funkcji f w przedziale <−1;1>. a) 6+x−2x² ≥ 0 −2x²+x+6 ≥0 2x² − x −6 ≤ 0 Δ=1+48=49

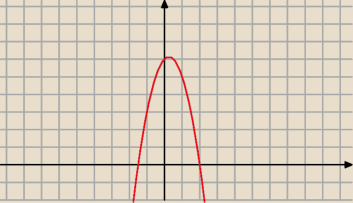
	1+7		1−7
x1=		=2 x2=		=−1,5
	4		4

x∊<−1,5 ; 2 > b) f(x)=√6+x−2x² Najmniejsza wartość wtedy, gdy w wyrażeniu pod pierwiastkiem będzie najmniejsza wartość

	−b		−1
xw=		=		=0,25
	2a		−4

	−Δ		−49
qw=		=		=6,125
	4a		−8

f(−1)=√6−1−2=√3 f(1)=√6+1−2=√5 Najmniejsza wartość funkcji to √3 dla x=−1 Największą wartość funkcji f w przedziale <−1;1>. Tutaj nie wiem jak ?

Godzio: Największa to √6,125

Piotr 10: A no tak potem jeszcze to pierwiastkuje się i dlatego mi się nie zgadzało z odp. Dzięki

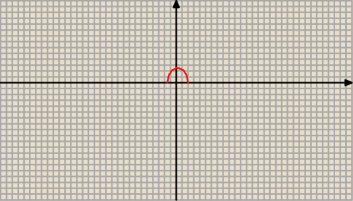Janek191: Największa wartość funkcji f będzie wtedy, gdy w wyrażeniu pod pierwiastkiem będzie największa wartość. f(x) = √ − 2 x² + x + 6

	−1		1
p =		=		∊ < − 1 ; 1 >
	−4		4

	1		1		1		2		1		49
q = − 2*(		)2 +		+ 6 = −		+		+ 6 = 6		=
	4		4		8		8		8		8

czyli

	49		7		7√2
ymax = √		=		=
	8		2√2		4

oraz y_min = f(−1) = √ − 2*(−1)² − 1 + 6 = √3

Eta: