ekstrema Weronika: Umie tu ktoś obliczać ekstrema?

biedaczek: jo

Weronika: f(x)=x/x+1, powinno wyjść: funkcja rosnąca w całej dziedzinie, brak ekstremów, jednak nie wiem dlaczego.

PW:

	x		x+1−1		1
f(x) =		=		= 1 −
	x+1		x+1		x+1

Nie znam rachunku różniczkowego ale wiem z rozważań elementarnych, że

	1
g(x) =
	x

jest funkcją malejącą na (∞, 0) i malejącą na (0,∞). Malejącą na całej osi nie jest. Wobec tego malejąca na tych samych przedziałach jest funkcja

	1
h(x) = −		.
	x

Tym samym malejąca jest

	1
k(x) = −
	x+1

(na innych przedziałach, ale ma te same własności co h(x)).

	1
wniosek: f(x) = 1 −		jest malejąca na dwóch przedziałach. Malejąca na całej
	x+1

dziedzinie nie jest.

PW: Wyłączyłem uwagę, od 5. wiersza powinno być oczywiście "rosnąca". Po prostu narysuj te wykresy, przecież to widać − na poziomie liceum.

daras: poczytaj o funkcji homograficznej to ta twoja , w x= 1 ma asymptotę i dla y= 0

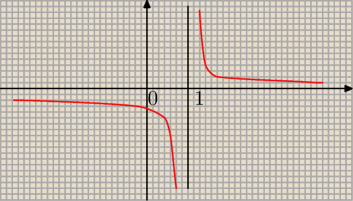
daras: tak to wygląda

daras: sry , oczywiście powinno być x = −1 i taka asymptota

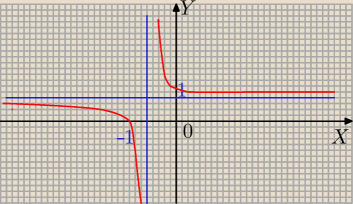
daras: teraz jest dobrze