Dowod
opo: Udowodnij,ze w trojkacie równobocznym ABC zachodzi rownosc |AX|+|BX|=|CX| , gdzie X jest
punktem wspólnym okręgu opisanego na trojkacie i prostej CX zawierającej wyskosc.
17 lis 18:45
opo: Bardzo proszę o rozwiązanie!

17 lis 18:54
Eta:
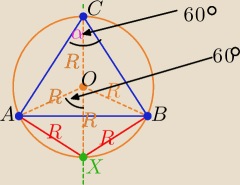
|<AOB|=2
α= 2*60
o to |<AOX|=|<BOX|= 60
o
|CX|=2R i trójkąty AOX i BOX są równoboczne o boku długości R
to:
|AX|+|BX|= 2R = |CX|
c.n.u
17 lis 19:10
ADA: Dziękuje Tobie dobry człowieku~!
17 lis 19:15

 |<AOB|=2α= 2*60o to |<AOX|=|<BOX|= 60o
|CX|=2R i trójkąty AOX i BOX są równoboczne o boku długości R
to:
|AX|+|BX|= 2R = |CX|
c.n.u
|<AOB|=2α= 2*60o to |<AOX|=|<BOX|= 60o
|CX|=2R i trójkąty AOX i BOX są równoboczne o boku długości R
to:
|AX|+|BX|= 2R = |CX|
c.n.u