rozwiąż nierówność dzdzownicsa:

x4 +2 x3 + x2
	<0
x − 1 +6 x2

MathGym: wyłącz w liczniku x² i zapisz L stronę jako iloczyn licznika i mianownika

bezendu:

x4+2x3+x2
	<0
6x2+x−1

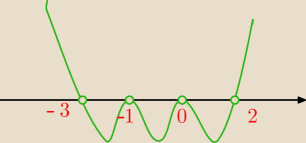
D=R\{−3,2} Δ=25 √Δ=5

	−1−5
x1=		=−3
	2

	−1+5
x2=		=2
	2

x²(x²+2x+1)(x+3)(x−2)<0 x²(x+1)²(x+3)(x−2)<0 x∊(−3,−1)∪(−1,0)∪(0,2)

PW: x⁴+2x³+x² = x²(x²+2x+1) = x²(x+1)² Dla x=0 lub x=−1 licznik jest równy 0, a więc nierówność nie jest spełniona. Dla pozostałych x licznik jest dodatni jako iloczyn kwadratów. Rozwiązań nierówności należy więc szukać wśród takich x, dla których mianownik jest ujemny: 6x²+x−1 < 0 ⋀ x≠0 ⋀ x≠−1