Okrąg 52: Mam do znalezienia równanie okręgu przechodzącego przez A i stycznego do prostej w pkt P. Jak to zrobić krok po kroku

irena_1: Środek okręgu leży na prostej prostopadłej do prostej stycznej i przechodzącej przez punkt P. Współrzędne środka spełniają więc równanie tej prostopadłej. Punkt S jest równo odległy od punktów A i P.

52:

	1
Ok tutaj mam treść zadania i obliczyłem że ta prosta prostopadła to y=−		−4,5 i dalej się
	x

zaciąłem. http://zapodaj.net/ae0d65cc0a96c.jpg.html

52:

	1
W sumie to tu można obliczyć r ego okręgu ale mam −		i nie wiem co tu wstawić do wzoru.
	x

52: Pomoże ktoś dalej ?

irena_1: A=(−1; 1) y=x−2, P=(4; 2) Prosta prostopadła ma równanie typu y=−x+k 4=−2+k k=6 Środek leży na prostej y=−x+6 S=(a, −a+6) |SA|=|SP| √(a+1)²+(−a+6−1)²=√(a−4)²+(−a+6−2)² (a+1)²+(5−a)²=(a−4)²+(4−a)² a²+2a+1+a²−10a+25=a²−8a+16+a²−8a+16 8a=6

	3
a=
	4

	3		21
−a+6=6−		=
	4		4

	3		21
S=(		;		)
	4		4

sprawdź jeszcze. r=|SA|

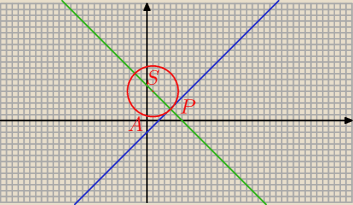Janek191: A = ( − 1; 1) y = x − 2 P = ( 4; 2) W punkcie P prowadzę prostą prostopadłą do danej prostej: 1 *a₂ = − 1 ⇒ a₂ = − 1 y = − x + b₂ 2 = − 4 + b₂ b₂ = 6 więc y = − x + 6 −−−−−−− Niech S − środek szukanego okręgu więc S = ( x; − x + 6) Jest on jednako odległy od A = ( −1; 1) i P = (4; 2), zatem I SA I² = I SP I² ( − 1 − x)² + ( 1 − ( −x + 6))² = ( 4 − x)² + ( 2 − ( − x + 6))² 1 + 2x + x² + ( x − 5)² = 16 − 8x + x² + ( x − 4)² 1 + 2x + x² + x² − 10 x + 25 = 16 − 8 x + x² + x² − 8x + 16 26 − 8x = 32 − 16x 16 x − 8 x = 32 − 26 8x = 6

	3
x =
	4

	3		1
y = −		+ 6 = 5
	4		4

czyli

	3		21
S = (		;		)
	4		4

	3		21		7		17
r2 = I SA I2 = ( − 1 −		)2 + ( 1 −		)2 = (−		)2 + (−		)2 =
	4		4		4		4

	49		289		338		1
=		+		=		=21
	16		16		16		8

Równanie okręgu:

	3		21		1
( x −		)2 + ( y −		)2 = 21
	4		4		8

===========================