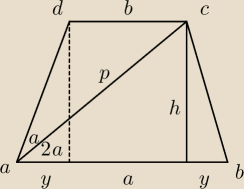
Wyznacz stosunek pól trójkątów,na które ta przekątna podzieliła trapez. wajdzik: Przekątna trapezu równoramiennego o podstawach AB,CD (|AB|>|CD|) tworzy z jego podstawą AB kąt 2α, a z ramieniem AD kąt α. Wyznacz stosunek pól trójkątów,na które ta przekątna podzieliła trapez.

PACD
PABC

	h
sin2α=
	p

	h
tg3α=
	y

h=y*tg3α

	h
tg2α=		⇒ h=(a−y)*tg2α
	a−y

	a−b
y=
	2

y*tg3α=a*tg2α−ytg2α ytg3α+ytg2α=atg2α y(tg3αa+tg2α)=atg2α

	atg2α
y=
	tg3α+tg2α

	2atg2α
a−b=
	tg3α+tg2α

	atg3α+atg2α−2atg2α
b=
	tg3α+tg2α

	tg3α−tg2α
b=a(		)
	tg3α+tg2α

Stosunek pól:

	tg3α−tg2α		tg3α−tg2α
a(		) : a =
	tg3α+tg2α		tg3α+tg2α

	sinα
w odpowiedziach jest wynik: P=
	5sinα

Czy gdzieś zrobiłem błąd Z góry dziękuję za pomoc

wajdzik:

wajdzik:

wajdzik: ponnawiam prośbę

MathGym:

	1
a nie lepiej próbować to liczyć ze wzoru na pole trójkąta P=		absinα
	2

wajdzik: MathGym, może i lepiej ale liczyłem tym sposobem, zrobiłem coś źle ?

wajdzik:

wajdzik: proszę o sprawdzenie

wajdzik:

wajdzik:

wajdzik:

Mila: Przekształcenia i wzory dobrze, masz inną postać wyrażenia, które należałoby przekształcić, ale nie warto, bo dużo rachunków. Może się pokuszę. Napisz odpowiedź z książki, bo chyba błędną podałeś.

Mila:

	b		sinα
Może		=
	a		sin(5α)

Mila: To masz to samo, przekształciłam. Nie ma dużo rachunków.(wzory z tablic)

tg(3α)−tg(2α)		sinα		sin5α
	=		:		=
tg(3α)+tg(2α)		sin(3α)*cos(2α)		sin(3α)*cos(2α)

	sinα
=
	sin(5α)

Moje rozwiązanie:

	1
PΔADC=		*p*c*sinα
	2

∡ACB=180−(2α+3α)=180−5α

	1		1
PΔACB=		*p*c*sin(180−5α)=		*p*c*sin(5α)
	2		2

PΔADC		1   *p*c*sinα 2		sinα
	=		=
PΔACB		1   *p*c*sin(5α) 2		sin(5α)

Mila: