wykazać że jest taka sama odległość bla bla: wykaż, że odległość dowolnego punktu paraboli y=x² os punktu (0,¹₄) jest taka sama jak odległość tego punktu od prostej y=−¹₄

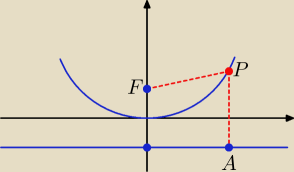
Bogdan: Parabola to zbiór punktów równo odległych od pewnej prostej (zwanej kierownicą paraboli) i pewnego punktu (ogniska paraboli) nie leżącego na tej prostej. W tym zadaniu ogniskiem jest punkt F(0, 1/4), kierownicą jest prosta y= −1/4. Punkt A(x, −1/4) należy na kierownicy. Bierzemy dowolny punkt paraboli y = x², niech to będzie punkt P(x, x²)

	1		1		1
|PF|2 = ( x − 0 )2 + ( x2 −		)2 = x2 + x4 −		x2 +		=
	4		2		16

	1		1
= x4 +		x2 +
	2		16

|PA|² = ... dokończ i porównaj z |PF|²

Bogdan: Nieładnie się zapisało, powtarzam. Parabola to zbiór punktów równo odległych od pewnej prostej (zwanej kierownicą paraboli) i pewnego punktu (ogniska paraboli) nie leżącego na tej prostej. W tym zadaniu ogniskiem jest punkt F(0, 1/4), kierownicą jest prosta y= −1/4. Punkt A(x, −1/4) należy do kierownicy.

bla bla: |PA|²=(x−x)²+(x²+¹₄)²=x⁴+¹₂x²+¹₁₆ |PF|²=|PA|² |PF|=|PA| Dziekuje bardzo, pozdrawiam

Bogdan: