geometria analityczna samouczek: dane są proste równoległe k i l. Prosta k przechodzi przez punkt A= (1,1) a prosta l− przez punkt B= (3,2). Odcinek wyznaczony przez punkty przecięcia tych prostych z osią Ox ma długość 2. Wyznacz równania prostych k i l. Rozważ dwa przypadki.

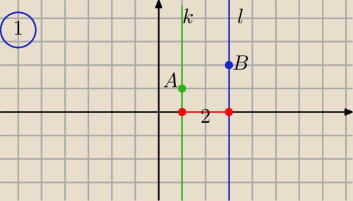
Eta: 1) przypadek proste k i l równoległe do osi OY k: x=1 , l: x= 3 bo odległość między nimi wynosi 2 2)przypadek k: y=ax+b i A(1.1)∊k ⇒ 1=a+b ⇒ b= 1−a to k: y= ax+1−a l: y=ax+c i B(3,2)∊l ⇒ 2=3a+c ⇒ c= 2−3a to l : y= ax+2−3a teraz odległość między miejscami zerowymi ( na osi OX) wynosi 2 czyli |x₁−x₂|= 2 miejsca zerowe

	a−1
dla k: ax+1−a=0 ⇒ x1=		, dla a≠0
	a

	3a−2
dla l : ax+2−3a=0 ⇒ x2=
	a

teraz z warunku |x₁−x₂|= 2 wyznacz "a"= ...... podstaw za "a" otrzymasz równania prostych :

	1		3
k: y=		x+
	4		4

	1		5
l : y=		x+
	4		4

Eta: 1) przypadek proste k i l równoległe do osi OY k: x=1 , l: x= 3 bo odległość między nimi wynosi 2 2)przypadek k: y=ax+b i A(1.1)∊k ⇒ 1=a+b ⇒ b= 1−a to k: y= ax+1−a l: y=ax+c i B(3,2)∊l ⇒ 2=3a+c ⇒ c= 2−3a to l : y= ax+2−3a teraz odległość między miejscami zerowymi ( na osi OX) wynosi 2 czyli |x₁−x₂|= 2 miejsca zerowe

	a−1
dla k: ax+1−a=0 ⇒ x1=		, dla a≠0
	a

	3a−2
dla l : ax+2−3a=0 ⇒ x2=
	a

teraz z warunku |x₁−x₂|= 2 wyznacz "a"= ...... podstaw za "a" otrzymasz równania prostych :

	1		3
k: y=		x+
	4		4

	1		5
l : y=		x+
	4		4