indukcja geometryczna z wartością bezwzględną po obu stronach równania
vipnastka: Hejka, czy ktoś mógłby mi rozpisać rozwiązanie na to zadanko: Ix−5I ≤ Ix+2I? jest z działu o
indukcji geometrycznej wartości bezwzględnej. Wszędzie podają tylko rozwiązania do zadań,
gdzie wartość bezwzględna jest tylko po 1 stronie równania, a po drugiej zwykła liczba,
natomiast nigdzie nie piszą jak jest w przypadku, gdy po obu stronach jest wartość
bezwzględna

proszę pomóżcie.
10 paź 21:27
vipnastka: sorki nie indukcji geometrycznej tylko geometrycznej interpretacji
10 paź 21:30
Bogdan:
Wchodzę, bo mecz mnie nudzi.
10 paź 21:48
fik-mik:

10 paź 21:50
Bogdan:
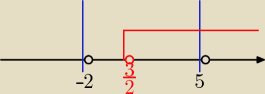
Można różnie, przedstawiam jeden ze sposobów.
|x − 5| ≤ |x + 2|
Dla x∊(−
∞, − 2): −(x − 5) ≤ −(x + 2) ⇒ −x +5 ≤ −x − 2 ⇒ 7 ≤ 0, sprzeczność.
| | 3 | |
Dla x∊<−2, 5): −(x − 5) ≤ x + 2 ⇒ −x + 5 ≤ x +2 ⇒ 2x ≥ 3 ⇒ x ≥ |
| ⇒ |
| | 2 | |
Dla x∊<5, +
∞): x − 5 ≤ x + 2 ⇒ 0 ≤ 7 ⇒ x∊<5, +
∞)
10 paź 22:05
Bogdan:
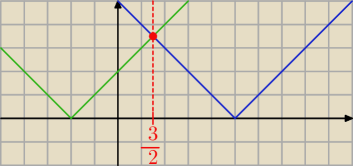
Można też tak:
y = |x − 5| (niebieski wykres)
y = |x + 2| (zielony wykres)
|x − 5| ≤ |x + 2|
| | 3 | |
Widzimy, że niebieski wykres ma punkt wspólny z zielonym dla x = |
| oraz jest pod |
| | 2 | |
zielonym
| | 3 | | 3 | |
dla x > |
| , a więc |x − 5| ≤ |x + 2| dla x ≥ |
| |
| | 2 | | 2 | |
10 paź 22:15
 proszę pomóżcie.
proszę pomóżcie.

 Można różnie, przedstawiam jeden ze sposobów.
|x − 5| ≤ |x + 2|
Dla x∊(−∞, − 2): −(x − 5) ≤ −(x + 2) ⇒ −x +5 ≤ −x − 2 ⇒ 7 ≤ 0, sprzeczność.
Można różnie, przedstawiam jeden ze sposobów.
|x − 5| ≤ |x + 2|
Dla x∊(−∞, − 2): −(x − 5) ≤ −(x + 2) ⇒ −x +5 ≤ −x − 2 ⇒ 7 ≤ 0, sprzeczność.
 Można też tak:
y = |x − 5| (niebieski wykres)
y = |x + 2| (zielony wykres)
|x − 5| ≤ |x + 2|
Można też tak:
y = |x − 5| (niebieski wykres)
y = |x + 2| (zielony wykres)
|x − 5| ≤ |x + 2|