ZW
bezendu:
| | 2|x|−1 | |
Jak wyznaczyć zbiór wartości bez rysowania f(x)= |
| |
| | |x|+1 | |
Mam rozważać na dwa przypadki x≥0 i x<0. Czy jakiś inny sposób ?
16 lis 22:48
Godzio:
| 2|x| − 1 | | 2(|x| + 1) −3 | | 3 | |
| = |
| = − |
| + 2 |
| |x| + 1 | | |x| + 1 | | |x| + 1 | |
f(0) = − 1
A jak x sobie rośnie (bądź maleje, na jedno wychodzi) to co się dzieje z wartością ?
16 lis 22:52
bezendu:
Wartość się zmienia.
16 lis 22:53
Eta:
| | 2(|x|+1)−3 | | 3 | |
f(x) = |
| = 2− |
| |
| | |x|+1 | | |x|+1 | |
16 lis 22:53
bezendu:
ZW=R\{2} ?
16 lis 22:55
Godzio:
To, że się zmienia to oczywiste
R na pewno nie, bo nie osiąga wartości mniejszych od −1
16 lis 22:57
bezendu:
ZW=<−1,2) ?
16 lis 22:57
Godzio:
16 lis 22:58
Godzio:
Można też tak:
f(x) = m i szukamy m takiego, że to równanie ma rozwiązanie
16 lis 22:58
bezendu:
A graficznie tak jak podałem w tych przedziałach ?
16 lis 23:01
Mila:
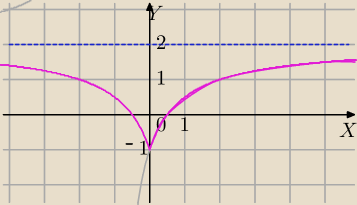
Rozważasz jeden przypadek:
x≥0 i tylko ta część wykresu Cię w pierwszym etapie interesuje.
y=2 asymptota pozioma ,
Część wykresu f(x) z prawej strony OY " odbijamy "symetrycznie względem OY
f(0)=−1
Z
w=<−1,2)
Łatwo odczytasz ile rozwiązań ma równanie:
f(x)=m w zależności od m.
16 lis 23:29
bezendu:
Czemu tylko jeden przypadek ?
16 lis 23:36
Mila:
f(|x|) rysujemy odbijając część wykresu funkcji f(x) z prawej strony OY, pozostała część
wykresu nie interesuje nas.
16 lis 23:41
bezendu:
odbijam symetrycznie ponieważ mam wartość bez ?
16 lis 23:43
Mila: Tak.
16 lis 23:45
bezendu:
Dziękuję i dobranoc
16 lis 23:50
Mila:
Dobranoc
17 lis 00:17