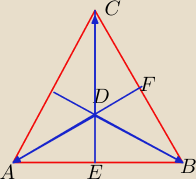
. Piotr 10: Udowodnij, ze jeżeli punkt D jest środkiem ciężkości trójkąta ABC to DA^→+DB^→+DC^→=0^→ Środek ciężkości dzieli każdą środkową w stosunku 2:1. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości. DA^→=DE^→+EA^→ DB^→=DF^→+FB^→ DC^→=DF^→+FC^→ DC^→= −2*DE^→ DF^→= −0,5*DA^→ FC^→= − FB^→ DE^→+EA^→+DF^→+FB^→+DF^→+FC^→=0^→ DE^→+2DF^→+EA^→+FB^→+FC^→=0^→ DE^→+EA^→+2DF^→+FB^→+FC^→=0^→ DA^→+2*( −0,5*DA^→)+FB^→+FC^→=0^→ FB^→+FC^→=0^→ FB^→ − FB^→=0^→ 0=0 Wykonując ciąg równoważnych przekształceń doszedłem do wniosku, że równość końcowa jest prawdziwa, a więc równość wyjściowa też musi być spełniona. OK?

Piotr 10: ?

biedaczek: Za taki dowód moja matematyczka ucięła mi punkty i napisała "manipulacja tezą" ale dlaczego to nie wiem

Godzio: Jest ok.

Piotr 10: Dzięki Godzio

Godzio: Może ja bym ciągnął po prostu równości, bo to, że piszesz ... = 0^→ to za dużo nie zmienia, ale strata czasu No i przy każdym powinno się pisać " ⇔"

Piotr 10: gdzie pisać ⇔? Ja na kompie to robię w tym programie i dlatego tak piszę trochę dziwnie, nie mogę jeszcze na kartce zwykłej, bo palec w gipsie

Piotr 10: A już wiem , dzięki