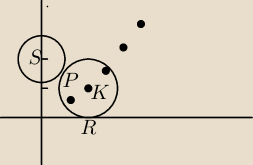 Równanie okręgu danego w postaci środkowej
x2 + (y − 2)2 = 1 okrąg o środku S(0,2) i promieniu r = 1
Szukany okrąg o środku K(x,y) z warunkiem PK = KR
PK = SK − SP = √x2 + (2 − y)2 − 1
KR = y
Stąd równanie
√x2 + (2 − y)2 − 1 = y
√x2 + (2 − y)2 = y + 1 Obustronnie do kwadratu
x2 + 4 − 4*y + y2 = y2 + 2*y + 1
Ostatecznie
x2 − 6*y + 3 = 0
Jest to parabola
Równanie okręgu danego w postaci środkowej
x2 + (y − 2)2 = 1 okrąg o środku S(0,2) i promieniu r = 1
Szukany okrąg o środku K(x,y) z warunkiem PK = KR
PK = SK − SP = √x2 + (2 − y)2 − 1
KR = y
Stąd równanie
√x2 + (2 − y)2 − 1 = y
√x2 + (2 − y)2 = y + 1 Obustronnie do kwadratu
x2 + 4 − 4*y + y2 = y2 + 2*y + 1
Ostatecznie
x2 − 6*y + 3 = 0
Jest to parabola

| x2+3 | ||
i y czyli x2+3=6y −−−> y= | ||
| 6 |
| x2+3 | ||
punkty na płaszczyźnie takie, że spełniają warunek (x, | ) | |
| 6 |
| X2+3 | ||
czy to w ten sposób wychodzi (x, | )? | |
| 6 |
| 1 | ||
Oczywiście parabola przesunięta wzdłuż osi Oy o | j | |
| 2 |
| 1 | 1 | |||
y = | *x2 + | |||
| 6 | 2 |