za (parę miesięcy) matura Saizou : matura task hejo wszystkim! Ma ktoś pod ręką jakieś 'fajne' zadania maturalne z wyjątkiem stereometrii Jak tak to ktoś mógłby coś wrzucić i na zachętę

ciekawsky: w jakim języku?

Saizou : po polsku jeśliś łaskaw

bezendu: Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, które przy dzieleniu przez 7 dają resztę 5.

MQ: Udowodnić, że suma wektorów, o początku w punkcie O i końcach w wierzchołkach A₁, A₂, ... A_n n−kąta foremnego, jest równa n*AS^→, gdzie S jest środkiem tego wielokąta.

Saizou : a₁=110 a_n=999 r=7 999=110+(n−1)7 n=128

	110+999
S128=		128=70 976
	2

krystek: W równoległoboku tgα kąta ostrego wynosi2,4, krótsza przekątna ma długośc 20cm a krótszy bok 13cm. Oblicz długość drugiej przekątnej

5-latek:

	1
Rozwiaz nierownosc (		)1−x/|x|≤1 nie moge tego zapisac ale ma byc 1/2 do potegi
	2

	1−x
		≤1
	|x|

zadanie nr 2 Dana jest funkcja f(x)=4−3x wykazac ze ciag f(1),f(3), f(5) ,........f(2n−1),......, jest ciagiem arytmetycznym . Zbadac monotonicznosc tego ciagu . zadanir nr 3 Udowodnic ze jesli x+y+z=90 stpni to tg2x+tg2y+tg2z=tg2x*tg2y*tg2z Na razie tyle bo trzeba isc spac

Saizou :

	12
tgα=
	5

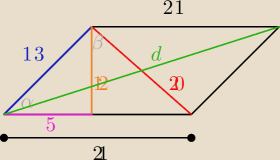
(12a)²+(5a)²=13²⇒a=1 z tw. cosinusów

	5
202=132+(5+b)2−2*13*		(5+b)⇒b=16
	13

	5
cosβ=−cosα=−
	13

	5
d2=132+212−2*13*21*(−		)
	13

d²=820 d=2√205

Saizou : zadanie 1 D: x∊R/{0}

	1
(		)1−x/lxl≤1
	2

2^x/lxl−1≤2⁰

x
	−1≤0 lxl>0
lxl

x−lxl≤0 x≤lxl⇒x∊R\{0}

Saizou : zadanie 2 f(x)=−3x+4 f(2n−1)=−3(2n−1)+4=−6n+7 f(2n+1)=−3(2n+1)+4=−6n+1 f(2n+1)−f(2n−1)=−6n+1+6n−7=−6= const zatem ciąg jest arytmetyczny i jego różnica wynosi −6. jest to ciąg malejący

tosia: dla jakich wartości parametru m równanie x²+2(m−3)|x|+m²−1=0 ma 3 różne rozwiązania? dla znalezionej wartości parametru m podaj rozwiązania tego równania

5-latek: Zbior rozwiazan zadania nr 1 jest wyznaczony zle. zadanie nr 2 dobrze

ICSP: I oczywiście coś ode mnie : 1^o Wyznacz wartości parametru m aby równanie miało rozwiązanie : sin(3x) = m * sin(x) 2^o Udowodnij że dla dowolnego x zachodzi :

x2 + 2
	≥ 2
√x2 + 1

3^o Równanie : 6^{(log₆ x)2} + x^{log₆ x} = 12 4^o Obliczyć :

(log6 3)2 + log6 16
log6 3 * log6 48 + (log6 4)2

I oczywiście mój faworyt : 5^o Rozwiązać nierówność w przedziale (π ; 2π)

	2
(		)sinx − 2cosx + 1 ≤ 31/2 + log0,75 (2√3)
	3

	2
log0,75		− gdyby nie było widać
	√3

Saizou : 5−latek błąd wynikał z tego że rozpatrzyłem inną potęgę

	1
(		)(1−x)/lxl≤1 x≠0
	2

2^x−1/lxl≤2⁰

x−1
	≤0
lxl

x−1≤0 x≤1 x∊(−∞:1>/{0}