jw Ania: Proszę o podpowiedź 2 √(1− x ) ( x − 3) > x−2 wychodzi mi przedział ((4−√2)/2 ; 4+√2)/2 ) w odpowiedzi mam przedział <1 ; 4+√2)/2 ) nie wiem skąd się wzięła ta jedynka. Ma to coś wspólnego z dziedziną ?

Bogdan: tim − wchodzisz ?

anmario: Zapewne ma to jakiś związek z dziedziną, bo zauważ, że dla x=0 po lewej stronie wychodzi pierwiastek z liczby −3, który liczbą rzeczywistą nie jest i jest lipa po całości. Z kolei dla x=2 mamy po lewej stronie pierwiastek z 1, czyli Twoja sugestia, że coś nie tak jest z dziedziną wydaje się być poprawną. Zatem co czynić? Ano rozwiązać jeszcze jedną nierówność, mianowicie: (1−x)(x−3)≥0 Co pozwoli wyszczególnić wszystkie iksy dla których pod pierwiastkiem znajdzie się tylko i wyłącznie liczba dodatnia (albo zero) Po porównaniu dziedziny z Twoim rozwiązaniem nierówności i wyrzuceniu z niego tych wartości x, które są poza dziedziną otrzymasz poprawne rozwiązanie.

Ania: z nierówności (1−x)(x−3)≥0 wychodzi mi, że x∊<1 , 3> , i to wyniku nie zmienia chyba coś źle licze

anmario: Źle Ci wychodzi, zauważ sama, że jeżeli z Twojego zbioru rozwiązań wybierzemy sobie 0 i wstawimy do nierówności wychodzi coś takiego: (1−0)(0−3)≥0 i dalej −3≥0 co prawdą nie jest a więc nierówność rozwiązana jest niepoprawnie. Najprawdopodobniej nie przekształciłaś nierówności wyjściowej do właściwej formy, czyl do tego: (x−1)(x−3)≤0 co prosto dostać mnożąc obie jej strony przez minus jeden by było być (x− coś) a nie (coś minus x), zobacz: (x−coś1)(x−coś2).... ≥0 to poprawna forma, dla metody jaką przyjęłaś a nie (coś1−x)(x−coś2)≥0. I kiedy już się z tym uporasz zastanów się dlaczego tak jest, to bardzo ważne.

Ania: a mając tę formę (x−1)(x−3)≤0 odczytuje miejsca zerowe x1 = 1 i x2= 3 ramiona parabili w gorę więc przedział mam x∊<1 , 3>

anmario: Aniu. Zapewne przeoczyłaś, że po pomnożeniu przez −1 zmienił się znak nierówności na przeciwny. Dodatkowo metoda, którą stosujesz niewiele ma wspólnego z tym, w którą stronę skierowane są ramiona paraboli (być może się mylę bo istnieje i taka, z tym, że bardzo zła, bo polega na wykuciu pewnych rzeczy "na pamięć" a nie na zrozumieniu mechanizmu) to metoda polegająca na badaniu znaku funkcji, która stoi po lewej stronie nierówności w przedziałach pomiędzy jej miejscami zerowymi. One, te znaki (dla funkcji ciągłych) są zawsze takie same. Postaram się w ciągu kilkunastu minut znaleźć coś odpowiedniego o rozwiązywaniu tego typu nierówności i podam Ci link.

anmario: Aha, zapomniałem potwierdzić, tak

Ania: bardzo dziękuję. A możesz mi rozwiązać krok po kroku to zadanie ? wiem, że to nie ładnie tak prosić o podane na tacy, ale może zrozumiem to lepiej. ps a znak zmieniałam przy pomnożeniu przez −1

anmario: Ania, teraz jestem nieco zajęty. Chętnie rozwiążę krok po kroku i więcej, pokażę Ci, jak trzeba sobie radzić z tego typu nierównościami w przypadku ogólnym, bo "na szybkiego" nie znalazłem nic co w tym temacie uważam za ok w internecie, ale proszę − czy to może być jutro? Około 18 powiedzmy?

Ania: oczywiście. Będę na forum punkt 18. I bardzo dziękuje za pomoc

anmario: Witaj(cie) O rozwiązywaniu nierówności Zastanów się nad tym jak (mniej więcej) będą wyglądać wykresy takich funkcji a) y=(x−1)(x−2) b) y=(x−1)(x−2)(x−3) c) y=(x−1)(x−2)(x−3)(x−4) Nie chodzi o precyzyjne przedstawienie ich przebiegu tylko o coś w rodzaju nie wiem, modelu, szablonu, w jaki każdy z tych wykresów musi się wpisywać by był w zgodzie ze wzorami tych funkcji. 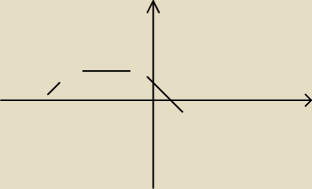Weźmy najpierw przykład a a) Funkcja z tego przykładu ma dwa miejsca zerowe x₁=1 bo y(1)=(1−1)(1−2)=0 i x₂=2 bo (2−1)(2−2) = 0. Czyli wykres tej funkcji musi, inaczej być nie może, przecinać oś OX w punktach x=1 i x=2. Co więcej znak funkcji musi zmienić się przy tym na przeciwny, skoro przeszła przez miejsce zerowe to znak zmienić musiała. Weźmy jakąś wartość x większą niż wartość jej największego miejsca zerowego, w tym wypadku jakieś x>2 i przez zwyczajne podstawienie do zadanego wzoru funkcji sprawdźmy tylko jej znak dla tego x. Przyjmijmy, że x =1000, to na pewno większe niż 2. y(1000)=(1000−1)(1000−2)= liczenie nie ma sensu interesujące jest tylko to, że y na pewno jest dodatnie. I co więcej będzie dodatnie dla każdego x>2 bo nie ma możliwości by ni stąd ni zowąd okazało się, że y jest ujemny jeżeli tylko rozpatrujemy wartości x większe niż dwa. By tak było, by y stał się ujemny potrzeba by wykres funkcji przeszedł przez miejsce zerowe przecież. Przypominam, że rozważamy funkcję ciągłą, to bardzo ważne zastrzeżenie, ale pojęcia ciągłości nie będziemy definiować by nie odrywać się od zasadniczego nurtu naszych rozważań. Dla naszych potrzeb przyjmijmy tylko, że ciągłość funkcji pociąga za sobą możliwość odrysowania jej wykresu bez konieczności odrywania ołówka od papieru. Zaprezentowany na rysunku wykres to oczywiście wykres funkcji nieciągłej bo nie istnieje możliwość narysowania go bez oderwania ołówka. Na razie kończę, ale piszę dalej, tylko zaraz będzie potrzebny drugi rysunek a nie wiem jak włożyć dwa w jeden post, nie wiem nawet czy da się to zrobić. Chętnie przeczytam uwagi na temat tego co piszę, bardzo teraz próbuję "przyłożyć" się do wyjaśnienia tego mało na ogół rozumianego przez przyszłych maturzystów tematu i chciałbym uniknąć niejasności lub wręcz błędów (brrrr) Za jakiś czas (1h najwyżej) cd

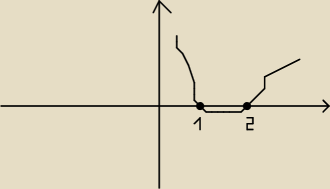
anmario: Zgodnie z tym co ustaliliśmy wykres funkcji z rozważanego właśnie przykładu musi mieć miejsca zerowe w x=1 i x−2 oraz y musi zmieniać znak przy przechodzeniu przez te miejsca bo dla funkcji ciągłej inaczej być nie może po prostu. A funkcja tego typu i ogólniej, wszystkie funkcje typu: y=(x−a)(x−b)(x−c)(x−d)... itd lub poprawniej, ale tak samo w sumie y=(x−x₁(x−x₂))(x−x₃).... (x−x−n) są ciągłe co przyjmijmy bez dowodu, tak po prostu jest (dowód oczywiście istnieje i nie jest trudny) Zatem, uogólniając, każda z takich funkcji zmienia znak przy przechodzeniu przez swoje miejsce zerowe co pozwala bez trudu rozwiązywać wszystkie nierówności typu: (x−x₁(x−x₂))(x−x₃).... (x−x−n)>0 (x−x₁(x−x₂))(x−x₃).... (x−x−n)<0 (x−x₁(x−x₂))(x−x₃).... (x−x−n)≤0 (x−x₁(x−x₂))(x−x₃).... (x−x−n)≤0 ponieważ, i tutaj znowu wróćmy do funkcji z przykładu, łatwo sporządzić model ich wykresu. Funkcja, którą rozważamy musi przebiegać jakoś tak jak pokazuje to rysunek na górze. Oczywiście Ty wiesz, że ten rysunek jest mocno nieprecyzyjny, że to parabola powinna być przecież, ale przypominam, że interesuje nas model tylko, szczegóły ważne tutaj nie są. Ona musi tak jakoś biegnąć i koniec. Teraz w ramach ćwiczenia, korzystając tylko i wyłącznie z przedstawionego przeze mnie wykresu, spróbuj określić kiedy: y>0 y<0 y≥0 y≤0 pamiętając, że zgodnie ze wzorem y=(x−1)(x−2) Działaj

Ania: co do tego fragmetu to mam tylko jedno pytanie. cytuje "Co więcej znak funkcji musi zmienić się przy tym na przeciwny, skoro przeszła przez miejsce zerowe to znak zmienić musiała." tego właśnie nie rozumiem. czyli dla x ∊ (−∞, 1)U(2, +∞) funkcja przyjmuje wartości dodatnie zmiana znaku odwróci wykres i wartości dodatnie będą tylko w przedzile (1,2) jeśli tylko mieszam to przepraszam...

Ania: y>0 dla x (−∞, 1)U(2, +∞) y<0 dla x (1,2) y≥0 dla x (−∞, 1>U<2, +∞) y≤0 dla x <1,2> tak ?

anmario: Zgadza się Lecę dalej, zejdzie następna godzina niestety Ale może przyda się tak "raz na zawsze", dla wszystkich

anmario: Najpierw odpowiem na Twoje pytanie: Zmiana znaku po przejściu przez miejsce zerowe powoduje, że funkcja przebiega po wartościach dodatnich jeżeli przedtem biegła po ujemnych i odwrotnie, a nie, że wykres się "odwraca". Być może myślisz dokładnie tak jak napisałem, ale nieprecyzyjnie się wyrażasz, nie wiem. Naprawdę cieszę się jednak, że ogarniasz to, to widać "gołym okiem". Piszę dalej

Ania: już rozumem. Czekam na kolejne instrukcje

Ania: a pod słowem zmiana znaku, myślałam o zmianie znaków we wzorze funkcji. Np przy mnożeniu przez (−1). jeśli "a" było dodatnie zmienia się na ujemnie i wtedy odwracamy wykres. Pewnie znów niejasno piszę. Ale już rozumiem o co tam chodziło

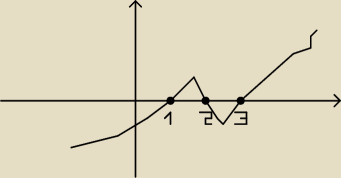
anmario: Zatem aby rozwiązać nierówność typu (x−a)(x−b)>0 albo podobną, wystarczy sporządzić model wykresu funkcji stojącej po lewej stronie nierówności, w przypadku powyżej funkcji y=(x−a)(x−b) i rozstrzygnąć kiedy y jest większe od zera. Co więcej identycznie jest dla innych tego typu nierówności co wynika z poprzednich rozważań. Dla ilustracji zajmijmy się przypadkiem b) b) y=(x−1)(x−2)(x−3) funkcja ma trzy miejsca zerowe x₁=1, x₂=2 i x₃ =3 Dla x=1000 (wybieramy jakąś liczbę "na prawo' od ostatniego miejsca zerowego, wszystko jedno jaką) y jest dodatnie, przy przejściu przez miejsca zerowe musi zmieniać znak, więc wykres wygląda mniej więcej tak jak na rysunku powyżej. Jak teraz wyglądają rozwiązania nierówności: y>0 y<0 y≥0 y≤0 To pytanie do Ciebie, zapewne wiesz od razu, ale czekam na odpowiedź

Ania: y>0 dla x (1,2)U(3.+∞) y<0 dla x (−∞,1)U(2,3) y≥0 dla x <1,2>U<3, +∞) y≤0 dla x (−∞.1>U<2,3> dobrze ?

anmario: Bardzo dobrze. To zbliżamy się do happy endu. Pół godzinki poproszę, piszę resztę

Ania: super

anmario: Rozważanie przykładu c możemy więc sobie darować, wszystko będzie dokładnie tak samo. Ale uogólnijmy. Wyszło na to, że mamy narzędzie do rozwiązywania nierówności typu f(x)>0 i podobnych jeżeli tylko funkcja f(x) jest iloczynem dwumianów typu (x−x_i), czyli nierówności typu: (x−x₁)(x−x₂)(x−x₃)....(x−x_n)>0 lub gdy wyrażenie po lewej jest mniejsze od zero, mniejsze lub równe lub większe lub równe. By rozwiązać taką nierówność wystarczy tylko sporządzić szkic wykresu funkcji y=(x−x₁)(x−x₂)(x−x₃)....(x−x_n) i odczytać z niego odpowiednie przedziały. Jednak jest pewna niejasność. Co będzie, jeżeli rozważana funkcja ma podwójne miejsce zerowe? Dla przykładu, jeżeli rozważamy nierówność: (x−1)(x−2)(x−2)>0 Czy nadal będzie tak samo? Otóż nie. Już pobieżna analiza wskazuje, że wykres funkcji przy przejściu przez x=2, czyli przez miejsce, które jest jakby "podwójnym" miejscem zerowym (tak pisać nie należy, prawidłowo jest, że przechodzi przez miejsce, które jest podwójnym pierwiastkiem tej funkcji, jednak nie używa się tej terminologii w stosunku do miejsc zerowych, one zawsze, jeżeli są, są pojedyncze, ale to tylko taka uwaga formalna w sumie) ... więc, wracając do tematu, już pobieżna analiza pokazuje, że tutaj będzie inaczej. Funkcja znaku tu nie zmieni, mówimy, że w takim przypadku wykres "odbija się " od tego miejsca zerowego i wygląda, mniej więcej tak jak na rysunku powyżej. Co więcej tak jest zawsze kiedy mamy do czynienia z parzystokrotnym miejscem zerowym (przypominam o uwagach w poprzednim nawiasie ) czyli, dla przykładu: (x−1)(x−2)(x−2)>0 (x−1)(x−2)²>0 − to oczywiście dokładnie to samo co to wyżej (x−1)(x−2)⁴>0 (x−1)(x−2)⁶>0 i tak dalej, zawsze, jeżeli tylko wykładnik potęgi do której podniesiony jest dwumian jest parzysty wykres od takiego miejsca zerowego po prostu się "odbije". Kiedy natomiast wykładnik jest nieparzysty, sytuacja się nie zmienia, czyli dla nierówności typu: (x−1)(x−2)³>0 (x−1)(x−2)⁵>0 wszystko jest tak jak widzieliśmy na początku, funkcja po przejściu przez miejsce zerowe zmienia znak. Zatem gdybyśmy mieli do rozwiązania nierówność (x−1)(x−2)²≤0 jak to zrobimy? Przypominam, że wykres funkcji y=(x−1)(x−2)² jest na górze tego posta Działaj Jeżeli coś nie jest jasne to oczywiście pytaj.

anmario: Chyba zamęczyłem Anię Nie mam już czasu Aniu, jeżeli chcesz dokończymy jutro, też mniej więcej około 18. Jeżeli nie chcesz bo już dokładnie wszystko pojęłaś, albo chcesz popatrzeć na inne źródła to oczywiście nie ma sprawy Pozdrawiam

Ania: dziękuję bardzo za pomoc, musiałam wpuścić siostrę bo robiła projekt na angielski i mnie nie było. Na spokojnie przeanalizuje. z Chęcią jutro się odezwę. Jeszcze raz bardzo Ci dziękuje.

Ania: przy pierwiastkach parzystych wykres nie przechodzi, gdyby było (x −1)(x−2)(x−2)(x−2) to już by przeszedł. jeśli tak jest , to wszystko rozumiem

anmario: Ano tak jest właśnie a swoje zadanie, to od którego wszystko się zaczęło, możesz teraz spokojnie rozwiązać sama, nie ma przecież w tej nierówności pierwiastków podwójnych. Tylko pamiętaj o tym, że czynnikami, który tworzą funkcję jaką rozważamy są wyrazy typu x−a a nie a−x, tak dla siebie możesz spróbować samodzielnie przeanalizować jaka to różnica, ale to jak chcesz, jutro i tak wspomnę o tym na pewno.