Okregi Wojtek: Bardzo proszę o pomoc. Okrąg o równaniu x² + y² − 2x + 4y − 20 = 0 przekształcono przez symetrię środkową względem punktu S=(3,1). Napisz równanie otrzymanego obrazu. Podaj ilustrację graficzną zadania.

anmario: Najlepiej to chyba napisać równanie tego okręgu w postaci: (x−a)²+(y−b)²=r² czyli w postaci, w której jawnie dany jest jego środek O(a,b) i promień r. Dla zadanego okręgu będzie: (x−1)²+(y+2)²=5² Teraz wystarczy skorzystać ze wzorów na obrazy punktu w symetrii środkowej, przy czym wystarczy poznać współrzędne przesuniętego środka, promień się nie zmieni bo symetria środkowa jest izometrią, czyli przekształceniem zachowującym odległość punktów. Pozdrawiam Przy okazji pozdrowienia dla Ety, Basi, Bogdana i oczywiście Jakuba

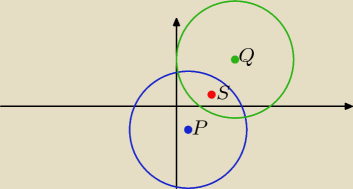
Bogdan: Środek okręgu P = (1, −2), długość promienia r = √1 + 4 + 20 = 5 Q = (x_Q, y_Q) − środek nowego okręgu

	xQ + 1
S = (3, 1) jest środkiem odcinka PQ, stąd 3 =		⇒ xQ = 5,
	2

	yQ − 2
oraz 1 =		⇒ yQ = 4.
	2

Q = (5, 4) Równanie nowego okręgu: (x − 5)² + (y − 4)² = 25 ⇒ x² + y² − 10x − 8y + 16 = 0

Bogdan: Witaj anmario

Wojtek: Dziękuje bardzo