Podstawą graniastosłupa prostego jest romb o przekątnych długości 30 cm i 10√3 c kacper34: Podstawą graniastosłupa prostego jest romb o przekątnych długości 30 cm i 10√3 cm. Wysokość tego graniastosłupa stanowi 60 % długości jego dłuższej przekątnej podstawy. Oblicz długości: a. krawędzi podstawy b. wysokości c. przekątnych tego graniastosłupa

wredulus_pospolitus: b) wysokość to 60% dłuższej przekątnej (czyli której) a) z tw. Pitagorasa c) mając wysokość ... z tw Pitagorasa

kacper34: Dłuższej przekątnej czyli w tym wypadku to dłuższą jest 30 cm

wredulus_pospolitus: dokładnie

kacper34: to nie ma chyba róznicy

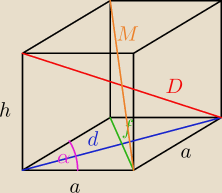
dero2005: d = 30 cm f = 10√3 cm

	f		√3
tgα2 =		=
	d		3

α = 60^o

	d*f
P = a2sinα =
	2

a = 10√3 h = 60%d = 18 cm D = √h² + d² = M = √h² + f² =

kacper34: a jak obliczyć pod punkt a z twierdzenia pitagorasa ?

dero2005: (^d₂)² + (^f₂)² = a² 15² + (5√3)² = a² 225 + 75 = a² a² = 300 a = √300 = 10√3