.
Piotr 10: Naszkicuj wykres funkcji f(x)=sInIxI+IsinxI w przedziale <−2π;2π>.
sinx ≥0 dla x∊ <−2π;−π>∪<0;π>∪ {2π}
sin x < 0 dla x∊(−π;0)∪(π;2π)
sinIxI ⇒ sinx dla x∊<0;2π> ⇒sin(−x) dla x∊(−2π;0)
f(x)= sinx+sinx=2sinx dla x∊<0;π>∪ {2π}
f(x)= sinx − sinx=0 dla x∊(π;2π)
f(x)=sin(−x)+sinx=−sinx+sinx=0 dla x∊ (−2π;−π)
f(x)=sin(−x) − sinx= −2sinx dla x∊(−π;0)
Chciałbym spytać się czy to jest w ogóle dobrze
14 lis 16:26
mephiu: tak
14 lis 16:29
Piotr 10: Może ktoś to jeszcze potwierdzić ?
14 lis 17:17
ZKS:
Zjadłeś jeszcze f(x) dla x = −2π.
14 lis 17:22
wredulus_pospolitus:
A nie łatwiej to po prostu narysować

sin|x| to nic innego jak sinx dla x∊<0,2π> i odbity na ujemną stronę
|sinx| to nic innego jak sinx i ujemne 'y' odbite do góry
więc będzie:
2sinx dla x∊<−π, π>
i 0 dla pozostałej części
14 lis 17:25
Piotr 10: f(x)=sin(−x)+sinx=0 dla x∊<−2π;−π) , tak? (( 3 f(x) u mnie ))
14 lis 17:29
wredulus_pospolitus:
Piotr ... narysuj sobie te dwie funkcje na jednym układzie
zobaczysz gdzie się 'znoszą' a gdzie 'nakładają'
14 lis 17:30
Piotr 10: Ciężko mi narysować, bo mam palec uszkodzony, jeśli mógłbyś narysować ten wykres tutaj, to bym
sprawdził sobie, czy dobrze myślę
14 lis 17:33
wredulus_pospolitus:
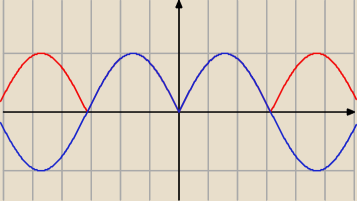
niestety tutaj 'przerywaną wykresu nie zrobię ... ale w części <−π,π> wykresy nachodzą na
siebie
|sinx|
sin(|x|)
14 lis 17:34
ZKS:
Dla x = 2π oraz x = π też masz f(x) = 0.
14 lis 17:34
ZKS:
Ale Twój zapis jest poprawny.

14 lis 17:37
wredulus_pospolitus:
i jak widzisz ... dla <−2π,−π> ∪<π,2π> te dwie funkcję się 'znoszą ... więc ich suma =0
a w <−π,π> się nakładają, więc ich suma da 2sin(|x|)
albo jak wolisz to:
<−π,0> masz −2sinx
<0,π> masz 2sinx
piszę domknięte wszędzie ... ale sobie pootwieraj tam gdzie chcesz
14 lis 17:38
Piotr 10: Ja trochę namotałem ze swoim rozwiązaniem z przedziałami.
wredulus pospolitus Twój dobry
sposób dziękuję za pomoc

14 lis 17:41
wredulus_pospolitus:
Piotr ... nie no ... masz dobrze ... tylko po prostu jak to zobaczyłem ... ile linijek wyliczeń
... to od razu pomyślałem − toć to graficznie można

14 lis 17:44
wredulus_pospolitus:
zwłaszcza, że masz to naszkicować i tak i tak

14 lis 17:45
Piotr 10: Nie rozumiem do końca co mam źle w swoim zapisie. Mógłbyś
ZKS napisać wszystko w jednym
poście

14 lis 17:52
wredulus_pospolitus:
Ale on jest poprawny
nie masz tylko uwzględnionego x=−2π
14 lis 17:53
Piotr 10: A ok. Dziękuję, jak wrócę od szpitala to jeszcze wrócę do narysowania tego wykresu
14 lis 17:55
ZKS:
Napisałem że Twój zapis jest jak najbardziej poprawny.

14 lis 17:55
ZKS:
Życzę szybkiego powrotu do formy.

14 lis 17:56
 sin|x| to nic innego jak sinx dla x∊<0,2π> i odbity na ujemną stronę
|sinx| to nic innego jak sinx i ujemne 'y' odbite do góry
więc będzie:
2sinx dla x∊<−π, π>
i 0 dla pozostałej części
sin|x| to nic innego jak sinx dla x∊<0,2π> i odbity na ujemną stronę
|sinx| to nic innego jak sinx i ujemne 'y' odbite do góry
więc będzie:
2sinx dla x∊<−π, π>
i 0 dla pozostałej części
 niestety tutaj 'przerywaną wykresu nie zrobię ... ale w części <−π,π> wykresy nachodzą na
siebie
|sinx|
sin(|x|)
niestety tutaj 'przerywaną wykresu nie zrobię ... ale w części <−π,π> wykresy nachodzą na
siebie
|sinx|
sin(|x|)






