trygonometria. wykres funkcji -2sinx. Kamil: Narysuj wykres funkcji f(x)= |sinx| −sinx dla x∊<−2π;2π>, a następnie narysuj wykres funkcji g(x)=f(|x|), dla tego samego przedziału. wiem, że trzeba rozpatrzyć dwa przypadki. 1. f(x)=sinx−sinx=0 dla x≥0 2. f(x)=−sin−sinx=−2sinx dla x<0 no i teraz utknąłem. nie ogarniam jak narysować wykres −2sinx. Mógłby mi ktoś wyjaśnić? Z g(x) sobie poradzę, to po prostu będą odpowiedzi dodatnie tylko czyli te po prawej stronie osiY, lecz nie kapuje jedynie tego −2sinx. Jak to narysować?

~r.: złe warunki: 1. f(x)=sinx−sinx=0 dla sinx≥0 2. f(x)=−sin−sinx=−2sinx dla sinx<0 teraz Ci coś innego wyjdzie

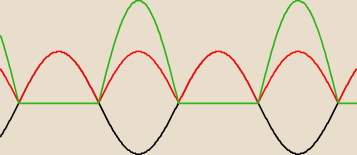
~r.: lepiej od razu graficznie: (czarny): sin(x) (czerwony): |sin(x)| (zielony): |sin(x)| − sin(x)

Kamil: Nie rozumiem tej metody graficznej, nic tu nie ogarniam

~r.: rysujesz sinusa (w odpowiednim przedziale); moduł z sinusa wygląda tak jak sinus tylko "garby" wszystkie ma do góry (bo moduł musi być >=0), różnica modułu i sinusa − tam gdzie " garby " się pokrywają (a więc funkcje mają takie same wartości) wychodzi 0 czyli wykresem jest "krecha" na osi OX, tam gdzie się nie pokrywają wychodzi 2sin(x) (sin(x)−(−sin(x))=sin(x)+sin(x), długi "garb))