symetralne trójkąta VIKI: symetralne trójkąta oblicz punkt przecięcia symetralnych boków trójkąta ABC A(1,2) B(3,7) C(−1,3)

Janek191: S₁ − środek odcinka AB pr AB prosta − symetralna odcinka AB ( prosta prostopadła do pr AB przechodząca przez S₁) S₂ − środek odcinka BC pr BC prosta − symetralna odcinka BC S − punkt wspólny symetralnych ( rozwiązać układ równań ).

Janek191: II sposób − wyznaczyć środek okręgu opisanego na Δ_ABC Korzystamy z wzoru: ( x − a)² + ( y − b)² = r²

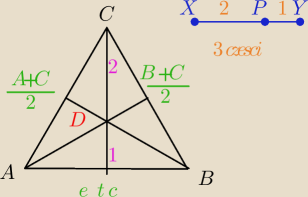
bolo: Wo0oW a nie można szybciej ? d− środek ciężkości bo tym właśnie jest punkt przecięcia się symetralnych.. czyli stosunek długości podzielonych odcinków 2:1

	2		1		1		2		B+C		A+B+C
czyli X		+Y		⇒ A		+		*		2 się skraca mamy		i tu
	3		3		3		3		2		3

podstawiamy dane punktów i dzielimy przez 3 i mamy współrzędne punktu D − środka ciężkości− przecięcia się środkowych

VIKI: dzięki, ale 2 sposób jak go wyznaczyć ? s to środek cięzkości czyli a i b ale jak z resztą ?

VIKI: w sensie s srodek okręgu ale jak dobrac x, y oraz r ?

Jolanta: najpierw obliczasz wspólrzedne środków boków boku AB

	xA+Xb		1+3
xs=		=		=2
	2		2

	yA+yB		2+7
yS=		=		=4,5
	2		2

symetralna przechodzi przez punkt S(2;4,5)i jest prostopadła do boku AB obliczasz wspólczynnik kierunkowy prostej na której lezy bok AB

	yB−yA		7−2		5
a=		=		=
	xB−xA		3−1		2

	2
symetralna jest prostopadła do tej prostej czyli ma a=−
	5

masz a ,wspólrzedne punktu korzystasz ze wzoru na prostą y−y₁=a(x−x₁)

	2
y−4,5=−		*(x−2)
	5

	2		4
y=−		x+		+4,5
	5		5

y=−U{2}[5}x+5,3 podobnie liczysz dla boku BC i AC póżniej punkt przecięcia symetralnych liczysz z układu równń

Janek191: @Bolo Środek ciężkości, to punkt przecięcia się środkowych trójkąta, a nie symetralnych. Ten trójkąt nie jest równoboczny !

Janek191: II sposób: A = ( 1; 2), B = ( 3; 7), C = ( − 1; 3) ( x − a)² + ( y − b)² = r² zatem 1) ( 1 − a)² + ( 2 − b)² = r² 2) ( 3 − a)² + ( 7 − b)² = r² 3) ( − 1 − a)² + ( 3 − b)² = r² czyli 4) 1 −2a + a² + 4 − 4b + b² = r² ⇒ a² + b² − 2a − 4 b + 5 = r² 5) 9 − 6a + a² + 49 − 14b + b² = r² ⇒ a² + b² − 6a − 14b + 58 = r² 6) 1 + 2a +a² + 9 − 6b + b² = r² ⇒ a² + b² + 2a − 6b + 10 = r² Od 5 ) odejmujemy 4) − 6 a + 2a − 14b + 4b + 53 = 0 Od 6) odejmujemy 4) 2a + 2a − 6b + 4b + 5 = 0 Mamy − 4a − 10 b = − 53 4a − 2b = − 5 −−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami − 12 b = − 58 / : (−12)

	5
b = 4
	6

−−−−−− więc

	5
4a − 2* 4		= − 5
	6

	2
4a − 9		= − 5
	3

	2		2
4a = − 5 + 9		= 4		/ : 4
	3		3

	1
a = 1
	6

−−−−−−−−−−

	1		5
S = ( a; b) = ( 1		; 4		)
	6		6

======================

Janek191: II sposób: A = ( 1; 2), B = ( 3; 7), C = ( − 1; 3) ( x − a)² + ( y − b)² = r² zatem 1) ( 1 − a)² + ( 2 − b)² = r² 2) ( 3 − a)² + ( 7 − b)² = r² 3) ( − 1 − a)² + ( 3 − b)² = r² czyli 4) 1 −2a + a² + 4 − 4b + b² = r² ⇒ a² + b² − 2a − 4 b + 5 = r² 5) 9 − 6a + a² + 49 − 14b + b² = r² ⇒ a² + b² − 6a − 14b + 58 = r² 6) 1 + 2a +a² + 9 − 6b + b² = r² ⇒ a² + b² + 2a − 6b + 10 = r² Od 5 ) odejmujemy 4) − 6 a + 2a − 14b + 4b + 53 = 0 Od 6) odejmujemy 4) 2a + 2a − 6b + 4b + 5 = 0 Mamy − 4a − 10 b = − 53 4a − 2b = − 5 −−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami − 12 b = − 58 / : (−12)

	5
b = 4
	6

−−−−−− więc

	5
4a − 2* 4		= − 5
	6

	2
4a − 9		= − 5
	3

	2		2
4a = − 5 + 9		= 4		/ : 4
	3		3

	1
a = 1
	6

−−−−−−−−−−

	1		5
S = ( a; b) = ( 1		; 4		)
	6		6

======================

Janek191: II sposób: A = ( 1; 2), B = ( 3; 7), C = ( − 1; 3) ( x − a)² + ( y − b)² = r² zatem 1) ( 1 − a)² + ( 2 − b)² = r² 2) ( 3 − a)² + ( 7 − b)² = r² 3) ( − 1 − a)² + ( 3 − b)² = r² czyli 4) 1 −2a + a² + 4 − 4b + b² = r² ⇒ a² + b² − 2a − 4 b + 5 = r² 5) 9 − 6a + a² + 49 − 14b + b² = r² ⇒ a² + b² − 6a − 14b + 58 = r² 6) 1 + 2a +a² + 9 − 6b + b² = r² ⇒ a² + b² + 2a − 6b + 10 = r² Od 5 ) odejmujemy 4) − 6 a + 2a − 14b + 4b + 53 = 0 Od 6) odejmujemy 4) 2a + 2a − 6b + 4b + 5 = 0 Mamy − 4a − 10 b = − 53 4a − 2b = − 5 −−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami − 12 b = − 58 / : (−12)

	5
b = 4
	6

−−−−−− więc

	5
4a − 2* 4		= − 5
	6

	2
4a − 9		= − 5
	3

	2		2
4a = − 5 + 9		= 4		/ : 4
	3		3

	1
a = 1
	6

−−−−−−−−−−

	1		5
S = ( a; b) = ( 1		; 4		)
	6		6

======================