Międzynarodowa Olimpiada Madzia: Na Międzynarodową Olimpiadę Matematyczną przyjechało 1000 osób. W sprawozdaniu podano, że wśród nich 811 włada językiem angielskim, 752 − językiem rosyjskim, 418 − językiem francuskim, 356 − językiem rosyjskim i francuskim, 570 − językiem rosyjskim i angielskim, 348 − językiem angielskim i francuskim, 297 osób mówi wszystkimi trzema językami. Wskaż, że w sprawozdaniu popełniono błąd.

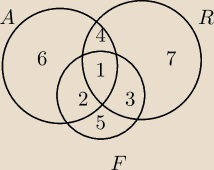
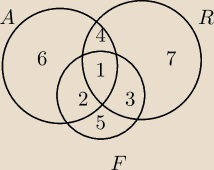irena_1: Wpisujesz w kolejne podzbiory: 1 − 297 2− 348−297=51 3− 356−297=59 4 − 570−297=273 5− 418−(297+51+59)=11 6 − 811−(297+273+51)=190 7 − 752−(273+297+59)=123 Dodaj teraz te wszystkie liczby: 297+51+59+273+11+190+123=1004 A powinno być 1000. Gdzieś więc popełniono błąd. Sprawdź jeszcze te moje rachunki. Ale o to mniej więcej chodzi.