Wykres
Kostek: | | |x2−1| | |
Jak będzie wyglądał wykres |
| |
| | x3−x | |
czy to też należy rozważać na przedziały ? Dziedzina będzie stała i licznik też ?
13 lis 17:24
krystek: | Ix2−1I | | Ix+1IIx−1I | |
| = |
| |
| x(x2−1) | | x(x+1)(x−1) | |
i teraz przeziały
D=R/{−1,01}
13 lis 17:28
Kostek:
1
0 (−
∞,−1)
ale w dwóch pozostałych również tak będzie wyglądał wykres ?
13 lis 17:31
PW: Może szybciej będzie
− to niebieskie się skraca dając wynik 1 lub −1 w zależności od znaku wyrażenia x
2−1.
Oczywiście jest to to samo, co napisała
krystek.
13 lis 17:34
Kostek:
ale licznik zawsze będzie taki sam chyba bo mam x2 ?
13 lis 17:38
13 lis 17:43
Kostek:
| | 1 | |
Mi się wydaję, że będzie tylko |
| ? |
| | x | |
13 lis 17:45
MQ: To ci się źle wydaje.
13 lis 17:48
Kostek:
ale ja mam w liczniku x2 a nie x ?
13 lis 17:51
PW: Jeszcze raz:
− to niebieskie się skraca dając wynik 1 lub −1 w zależności od znaku wyrażenia x2−1.
13 lis 17:51
MQ: W liczniku masz x2−1 a nie x2
13 lis 17:51
Kostek:
(−∞,−1) →x2−1
<−1,1>→x2−1
<1,∞)→x2−1
13 lis 17:57
Kostek: ?
13 lis 18:08
Mila:

D:
x
3−x≠0⇔x(x
2−1)≠0⇔x≠0 i x≠1 i x≠−1
1) |x
2−1|= x
2−1 dla x
2−1≥0 i x∊D⇔dla x<−1 lub x>1
Wtedy mamy:
2) |x
2−1|=−(x
2−1) dla x∊(−1,1)
Wtedy mamy:
13 lis 18:12
Kostek:
a jeszcze takie pytanie co jak tam w wartości bez stałby tylko x2 ?
13 lis 18:14
Mila:
Napisz funkcję.
13 lis 18:15
Kostek:
| | |x2| | |
Ja ogólnie pytam, nie chodzi mi o jakąś funkcję np mam takie coś |
| |
| | x−5 | |
13 lis 18:16
krystek: | | x2 | |
I co chcesz z tym zrobić? D=R/{5} y= |
| |
| | x−5 | |
13 lis 18:21
Mila:
|x2|=x2
13 lis 18:31
olaaaa: Heej, mam ogromną prośbę, czy ktoś mógłby rozwiązać mi sprawdzian z funkcji, podeślę na
gg/ maila. potrzebny bardzo pilnie...
13 lis 18:36
Kostek: chce zrozumieć to z tym x2 jak mam w module
13 lis 18:43
13 lis 18:48
krystek: Ale Ix2−1I już musisz rozpatrywać
13 lis 18:49
Kostek:
no właśnie skoro jest zawsze nie ujemne to skąd ten − u Pani Mili ?
13 lis 18:49
Kostek:
|x2−1|
10 (−∞,−1) np (−5)2−1=4 czy po opuszczeniu bez zmian
20 <−1,1) (−1)2−1=0 czyli również bez zmian
30 <1,∞) np 32−1=8 bez zmian
13 lis 18:51
krystek: 2) a wstaw x=0
13 lis 18:55
Kostek: ujemne ? ale dla −1 dodatnie ?
13 lis 18:56
krystek:
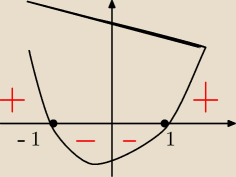
13 lis 18:57
Kostek:
a no tak bo dla drugiego powinno być (−1,1) i stąd moje błędy przepraszam za kłopot

13 lis 18:58
krystek: To p.Milę przeproś

13 lis 19:00
Kostek:
Przepraszam za zamieszanie

13 lis 19:03
Kostek: Ten drugi przedział jest niedobrze zapisany !
x∊(−1,1)/{0} Powinno być tak ?
16 lis 18:54
Aga1.: Tak.
16 lis 18:58
 D:
x3−x≠0⇔x(x2−1)≠0⇔x≠0 i x≠1 i x≠−1
1) |x2−1|= x2−1 dla x2−1≥0 i x∊D⇔dla x<−1 lub x>1
Wtedy mamy:
D:
x3−x≠0⇔x(x2−1)≠0⇔x≠0 i x≠1 i x≠−1
1) |x2−1|= x2−1 dla x2−1≥0 i x∊D⇔dla x<−1 lub x>1
Wtedy mamy:



 !
!



