Równoległobok beatka: 1. W równoległoboku ABCD wysokość DE ma 8cm i dzieli bok AB na odcinki dłgości: |AE| = 4,5cm, |EB| = 6cm. Oblicz długości przekątnych tego równoległoboku. 2. W równoległoboku ABCD kąt przecięcia przekątnych AC i BD ma miarę 60 stopni. Na dłuższej przekątnej AC zaznaczono punkt E w taki sposób, że odcinek DE jest prostopadły do przekątnej AC, Wiedząc, że |DE|= √3 oraz |∡ADE| = 45 stopni, oblicz długość przekątnych równoległoboku.

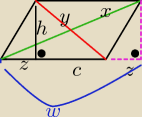
lila: z=4,5 8²+6⁼y² w=4.5*2+6=15 c=6 64+36=y² y²=15²+8² h=8 y=√100 y=√289 w=2*z+c y=10 y=17