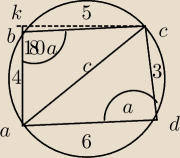
Oblicz odległość wierzchołka C od boku AB. wajdzik: Witam, Dany jest czworokąt o bokach |AB|=4, |BC|=5, |CD|=3, |AD|=6. Wiadomo ponadto, że można na nim opisać okrąg. Oblicz odległość wierzchołka C od boku AB. AC²=4²+5²−2*4*5*cos(180−α) AC²=6²+3²−2*3*6*cosα 41+40cosα=45−36cosα 76cosα=4

	1
cosα=
	19

sin²α+cos²α=1

	6√10
sinα=
	19

KC
	=sinα
5

KC=5*sinα

	5*6√10		30√10
KC=		=
	19		19

Mam parę pytań co do tego zadania. 1. AC²=4²+5²−2*4*5*cos(180−α) Jak później liczę to wyrażenie to wychodzi mi tylko 40cosα, co się dzieje ze 180?

	KC
2.		=sinα
	5

Nie widzę tego z rysunku, dlaczego przez 5? Dlaczego tak? Wgl po co odcinek |KC|? 3. Czy jest łatwiejszy sposób? Z góry dziękuję za pomoc.

wajdzik: Ponnawiam prośbę.

wajdzik:

wajdzik:

wajdzik:

Bizon: Ad.1 ...wzory redukcyjne cos(180^o−α)=−cosα

Mila: ∡KBC=α jako przyległy do 180−α

	KC		KC
sinα=		=
	BC		5

KC− wysokość poprowadzona do boku AB. (odległość C od AB, to długość odcinka prostopadłego CK )

Bizon: ad.2. Nie rozumiem czego nie rozumiesz − Masz policzyć odległość wierzchołka C od boku AB ... skoro odległość ... to musisz poprowadzić prostopadłą z C do AB ... przetnie ona prostą przechodzącą przez A i B w punkcie K a odcinek KC to to czego szukasz

wajdzik: Ad.1 − wszystko jasne Ad.2 − mniej więcej rozumiem, dzięki wielkie