Twierdzenie
Maslanek:
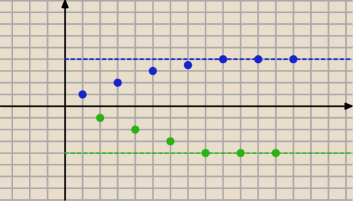
Problem z twierdzeniem:
(*) Jeżeli ciąg (a
n) jest zbieżny, to każdy jego podciąg jest zbieżny do tej samej granicy,
(**) Jeżeli z każdego podciągu ciągu (a
n) można wybrać podciąg zbieżny do g∊R\{±
∞), to a
n→g.
Pytanie: co jeśli z jednego z podciągów (a
n) można wybrać dwa różne podciągi zbieżne do róznej
granicy. Wtedy nie będzie on zbieżny, a więc (a
n) też nie powinien być zbieżny
Przykład wyżej.
Czyli znajduję podciąg podciągu (a
n) taki, że jest on rozbieżny. Cofając się do (*) podciąg
(a
n) jest rozbieżny, zatem i (*) (a
n) jest rozbieżny. Prawda?
Może źle zapisałem twierdzenie (**) na wykładzie
. W każdym razie szukałem kontrprzykładu do
tego co mam