Wzajemne położenie okręgu i prostej
vldd:
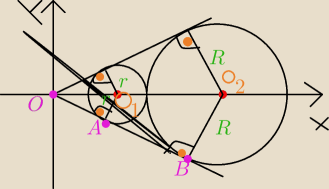
Okrąg o środku O
2 i promieniu R (rysunek obok) dany jest równaniem (x − 13)
2 + y
2 = 25
a) Oblicz długość odcinka OB.
b) Oblicz promień r okręgu o środku O
1 i wyznacz równanie tego okręgu.
Pomarańczowe kropki − kąt prosty.
Róźowe kropki − punkty
12 lis 18:45
vldd: Mógłby ktoś pomóc?
12 lis 19:59
Bizon:
...znasz 002 ... znasz R ... i znasz Pitagorasa ... ro znasz i OB
12 lis 20:09
vldd: Obliczyłem długość odcinka |0O|2, promień większego okręgu wziąłem ze wzoru i wyliczyłem |OB|
z Pitagorasa. Co z punktem b? Mógłbyś coś doradzić?
12 lis 20:29
Bizon:
... a Taleska też znasz? −
12 lis 20:31
vldd: Może coś z Talesa?
12 lis 20:31
vldd: No właśnie.
12 lis 20:32
vldd: Mamy |OO2| |O2B| i |OB|, potrzebujemy r.
Mamy mniejszy trójkąt i większy, który zawiera w sobie ten mniejszy. I jak tu teraz to ułożyć?
Jak próbuje ułożyć jakieś równanie, to mi wychodzą dwie niewiadome.
12 lis 20:38
Bizon:
znasz OO2 ... znasz R ... OO1 wyznaczysz pomocą R i r ... więc r policzysz
12 lis 20:38
vldd: Dobra, zabrałem się za liczenie. Punkt O(0,0), punkt O
2(13,0) Długość odcinka |OO
2| wyszła mi
13, prawidłowa odpowiedz to podobno 12.
12 lis 20:49
vldd: Ok, już wiem.
12 lis 20:51
vldd:
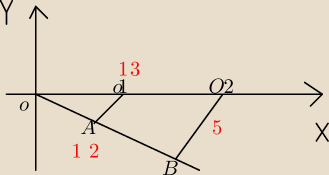
Został mi tylko podpunkt b.
OO1 OO2
−−−−− = −−−−−−
O1A OB
x 13
−−− = −−−−−
r 5
Skąd teraz wziąć x albo r, niestety nie zrozumiałem co napisałeś.
12 lis 20:59
vldd: Próbuje to obliczyć korzystając z a/(a+b) = x/y, ale ciągle mi wychodzą wyniki takiego typu:
13r=13r. Pomocy
12 lis 21:21
vldd: .
12 lis 21:45
vldd: Ostatni raz podbijam, jak nic nie da rady wymyślić to trudno.
12 lis 22:28
Bizon:
... chyba nie znasz jednak Talesa
12 lis 23:26