| 1 | ||
Zbadaj monotoniczność ciągu an=sin( | ) | |
| n |
to wystarczy
| 1 | π | |||
Od momentu, gdy | ≤ | jest malejący. | ||
| n | 4 |
| 1 | |
jest dodatnie i zmierza monotonicznie do 0. | |
| n |
| 1 | π | |||
Od n=2 | < | |||
| n | 4 |
| π | ||
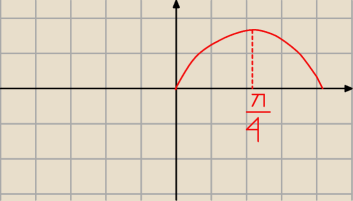
W zakresie <0, | > sin α jest też monotoniczna i wraz z α→0 maleje monotonicznie do 0. | |
| 4 |
| 1 | ||
A zatem od n=2 an=sin | jest malejący | |
| n |
| 1 | ||
sin | >sin{1}{2} więc dla każdego n jest to ciąg malejący | |
| 1 |
| 1 | 1 | |||
Oczywiście powinno być sin | >sin | |||
| 1 | 2 |
| π | ||
wybrałeś | | |
| 4 |
| 1 | 1 | |||
z tego : sin | −sin | | ||
| n+1 | n |
Dlatego
| π | ||
a nie | | |
| 2 |
| π | ||
∀x1,x2∊<0, | > x2<x1 ⇒ sin(x2)<sin(x1) | |
| 4 |
| 1 | π | 1 | 1 | 1 | 1 | |||||||
∀n≥2 | ∊(0, | ) ⋀ | < | ⇒ sin | <sin | |||||||
| n | 4 | n+1 | n | n+1 | n |
| 1 | ||
Wystarczy jeszcze zbadać przypadek, jak się ma sin | do sin{1}{2}, | |
| 1 |
| 1 | π | |||
bo | = 1 > | |||
| 1 | 4 |
masz rację
| 1 | π | |||
No to nie ma problemu, bo | < | , więc zachodzi dla wszystkich | ||
| 1 | 2 |
| π | ||
∀x1,x2∊<0, | > x2<x1 ⇒ sin(x2)<sin(x1) | |
| 2 |
| 1 | π | 1 | 1 | 1 | 1 | |||||||
∀n | ∊(0, | ) ⋀ | < | ⇒ sin( | )<sin( | ) | ||||||
| n | 2 | n+1 | n | n+1 | n |
| 1 | ||
aha czyli dla sinx mamy w tym przedziale że jest rosnący, a dla | jest malejący | |
| n |
