funkcja Radek: czy taka funkcja 3^x−1 ma asymptotę poziomą y=−1 ?

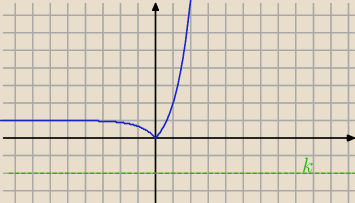
Radek: jak określić liczbę rozwiązań k∊(−∞,0) brak rozwiązań k∊{0} jedno rozwiązanie k∊(0,1) dwa rozwiązania k∊<1,∞) jedno rozwiązanie Czy podałem prawidłowe odpowiedzi ?

wredulus_pospolitus: 9:08 − tak ... ma (dla x−>−∞) 9:20 − tak pod warunkiem, że y=1 to asymptota pozioma ... druga sprawa −−− masz jako 'jedno rozwiązanie' podane dwa razy (połącz te zbiory)

Radek: k∊<1,∞)∪{0} ?

5-latek: Ale czy aby to jest wykres tej funkcji y=3^x−1 czy jakis z wartoscia bezwzgledna

Radek: f(x)=|3^x−1|

wredulus_pospolitus: Radek ... no i tak jest ok ... chociaż 'zgrabniej' wygląda to {0} ∪ <1,+∞)

Radek: A jeszcze proszę o wskazówkę do tego zadania: Ustal które z liczb 3,7,13,19 są dzielnikami liczby 5¹²−2¹² ?

5-latek: 5¹²−2¹²=(5⁶−2⁶)(5⁶+2⁶)= licz dalej skorzystalem ze wzoru a²−b² Tez dalej go wykorzystaj

wredulus_pospolitus: 5¹2 − 2¹2 = a¹2 − b¹2 = (a⁶−b⁶)(a⁶+b⁶) = (a³−b³)(a³+b³)(a⁶+b⁶) = = (a−b)(a²+ab+b²)(a³+b³)(a⁶+b⁶) = = (a−b)(a²+ab+b²)(a+b)(a²−ab+b²)(a²+b²)(a⁴−a²b²+b⁴) podstaw liczby ... bez problemu powyliczasz wartości w nawiasach (no może poza ostatnim)

5-latek: Czesc Artur przeciez ja zawsze mowilem ze Ty nie jestes taki i jak trzeba to pomozesz

wredulus_pospolitus: Witam 'o poranku' Oj tam oj tam ... to jest jeden z tych 'gorszych' dni spokojnie − do 12 się rozbudzę i wróci mi 'forma'

Radek: Dziękuję, do 12 już zrobię chyba swoje zadania