dla jakich a iza: dla jakich a układ równan ma dokladnie jedno rozwiazanie? |x|+|y|=a y=ax

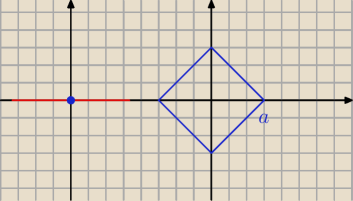
Godzio: Na rysunku przedstawiłem 2 sytuacje: Pierwsza dla a = 0 (warunek jest spełniony) Druga: a > 0 − nie da się poprowadzić funkcji y = ax, aby otrzymać tylko jeden punkt przecięcia Dla a < 0 mamy sprzeczność Odp: a = 0

iza: a ktoś może powiedzieć jak to "ładnie" zapisać?

Godzio: A to jest brzydko ? Można algebraicznie, milion przypadków, powodzenia

MQ: Dlaczego milion? |x|+|y|=a y=ax |x|+|ax|=a |x|+|a||x|=a |x|(1+|a|)=a

	a
|x|=
	1+|a|

Równanie |x|=k ma dokładnie jedno rozwiązanie, gdy k=0, zatem:

a
	=0 ⇔ a=0
1+|a|

Godzio: Rzeczywiście, myślałem, że będzie bardziej skomplikowane

Hugo: czy można było by to rozwiazać za pomocą 3 przypadków? x>0= y>=0 x>=0 y<0 x<0 y>=0 x<0 y<0 wyłaniając część wspólną, dużo się tez poskraca. znak równości daje się przy większości?

Hugo: 4* przypadków