funkcja wykładnicza bezendu: g(x)=2^x i f(x)=|2^x−2| w wyniku jakich przekształceń otrzymano wykres f(x) wiem, że o przesunięcie o wektor v^→[0,−2] ale jak opisać tą wartość bez ?

Piotr 10: f(x)=2^x →Translacja o wektor u^→=[0;−2] → 2^x − 2 → WbOX → I2^x−2I O to chodzi ?

bezendu: chodziło mi o to ''WbOX'' bo przekształcenie o wektor podałem przecież

Piotr 10: Jakbyś miał, np. 2^IxI to WbOY

bezendu: Ok dzięki

Mila: g(x)=2^x→^T_[0,−2]→h(x)=2^x−2→^S_OXy<0→f(x)=|2^x−2| y<0 napisać nad strzałką

bezendu: A wersja Piotrka nie jest dobra ?

Mila: Nie widziałam takiego zapisu. Zapis z 22:59 nie jest dobry.

Mila: Skąd Piotrze masz taki zapis?

bezendu: to jaki byłby dla 2^|x| g(x)=2^x→^S_oyx<0 ?

Piotr 10: Tak mnie uczyła zapisywać pani profesor ze szkoły. To co napisałem wyżej, to tak zawsze pisaliśmy( i piszemy) na lekcji

bezendu: ?

Hugo: Pani Mila zawszę prawdę ci powie

bezendu: Hugo ja o tym wiem ? Ale przeczytaj może najpierw moje pytanie ? 23:33 ?

Piotr 10: Nie chce nic mówić, ale ja tak zawsze miałem i mam na lekcji. Gdy mam, np. Ix−2I to rysujemy x−2 a potem nieraz pani mówi ''No to teraz WbOX''

Mila: Tak, tylko te zapisy są nad strzałką.

Mila: Myślę, że to taki mnemotechniczny sposób przekazywania wiedzy, jeśli dobrze narysujesz , to będzie zrozumiałe.

bezendu: ok dziękuję

Hugo: a pani Mila miała by chwilkę dla mnie? Potrzebuję się sprawdzić z prawdopodobieństwa warunkowego/całkowitego. Dzięki Tb się jej nauczyłem jednak chciałbym się sprawdzić na ile umiem. Ma pani jakieś heroiczne przykłady ?

bezendu: g(x)=2^|x+2| v[−2,0] i S_oy^x<0 ?

Piotr 10: Wpierw robimy tak 2^IxI →Translacja o wektor v^→=[−2;0]→2^Ix+2I

bezendu: wiem, że najpierw jest o wektor i tak podałem chodzi o tą wartość bez ?

Mila: Hugo, może jutro, teraz wybieram się spać. Przeczytałeś rozwiązania, które Ci napisałam do poprzednich zadań?

Piotr 10: Najpierw narzucamy na iks wartość bezwzględna. Jeżeli przesuniesz wpierw o wektor a potem narzucisz wartość bezwzględną ,to będzie źle

Hugo: Tak oczywiscie : ) Jednak spr jutro no nic ; / miłej nocki

bezendu: ale tak jak Ty mówisz to mam sytuacje typu f(x)=|x|+2 czyli mam o wektor [0,2] a ja mam 2^|x+2| ?

Piotr 10: Właśnie nie Jeżeli mam sytuacje typu f(x)=IxI+2 to wpierw robie x+2 a potem WBOY Jeżeli mam sytuacje typu f(x)=Ix+2I to wpierw robię, tak IxI a potem dopiero translacja o wektor

Piotr 10: Po prostu jeżeli chcemy przesunąć o wektor przy iksie to wpierw robimy WBOY

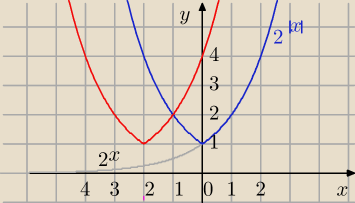
Mila: I sposób( najpierw |x|) y=2^x→^{S_oydla x>0}→y=2^|x|→T_[0,−2]→y=2^|x+2| Możesz sprawdzić tak : f(0)=2^|0+2|=4 f(−1)=2¹=2 f(−2)=2⁰=1 f(−3)=2¹=2 f(−4)=2²=4

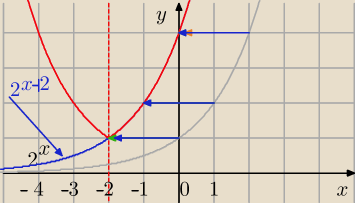
Mila: y=2^|x+2| I| sposób( najpierw translacja ) y=2^x→T_[0,−2]→2^x+2→(S_{x=−2 dla x>−2})→y=2^|x+2| S_{x=−2 dla x>−2} symetryczne odbicie względem prostej x=−2 tej części wykresu z prawej strony prostej

bezendu: f(x)=2^|x|+2 najpierw o wektor a potem S_oyx<0 ?

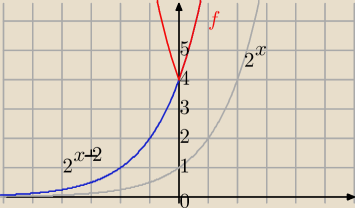
Mila: f(x)=2^|x|+2 Zgadza się . translacja, symetria względem OY wykresu z prawej strony, resztę pomijamy.

bezendu: Takie przekształcenia mogą być na maturze ? Przeważnie jest jakiś wykres i wartość bez ?

Mila: Może cos być, ale zawsze możesz weryfikować swój wykres, jak Ci pokazałam, możesz też rozpisywac.

bezendu: mam taką funkcję f(x)=6^x−6^−x jak wyznaczyć najmniejszą wartość tej funkcji ?

Lorak: Ta funkcja nie przyjmuje najmniejszej wartości.

Mila: Może masz podany przedział?

bezendu: Nie mam żadnego przedziału. I mam jeszcze to samo polecenie dla funkcji g(x)=3^x+3^−x

Piotr 10: A masz do tego może odpowiedź ?

bezendu: Nie. To zadanie mam z próbnego arkusza z mojej szkoły.

Lorak: To chyba Was nie lubią skoro dostajecie takie przykłady

bezendu: Chcą żebyśmy robili trudne a nie proste zadania

Lorak: ... a nawet niewykonalne

Piotr 10: Ja to coś wykombinowałem, ale nie wiem czy to w ogóle jest dobrze g(x)=3^x+3^−x

	1
g(x)=3x +(		)x
	3

	1		1		1
g(x)=(3x/2+(		)x/2)2 − 2*3x/2*(		)x/2=(3x/2+(		)x/2)2 − 2
	3		3		3

	1
(3x/2+(		)x/2)2≥0, gdy przesuniemy o wektor u→[0;−2] to otrzymamy funkcję g(x)
	3

−2 to najmniejsza wartość funkcji, ale czy to ok to nie wiem

Saizou : a na pewno tam jest 6^x−6^−x

Lorak: bezendu, może w pierwszym wzorze był plus zamiast minusa? Wtedy będzie najmniejsza wartość.

bezendu: Na pewno jest −

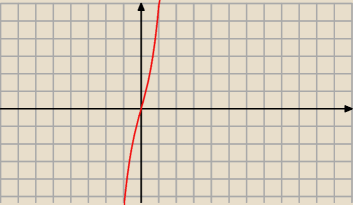
Saizou : nie mam najmniejszej wartości

Piotr 10:

	1
Źle to co napisałem, bo (3x/2+		x/2)2 > 0, więc to nie będzie miało najmniejszej
	3

wartości

Mila: 3^x=t, t>0

	1
f(t)=t+
	t

	1		1
t+		≥2 dla każdego t>0 [ t+		=2 dla t=1]
	t		t

bezendu: Czyli najmniejsza wartość to 2 ?

Saizou : ale zobacz jaką funkcję rozpatrzyła Mila z plusem

Mila: f(x)=3^x+3^−x ma wartość najmniejszą równą 2 dla x=0

bezendu: Dziękuję

Saizou : czyli jednak z plusem

Saizou : sorry niedopatrzenie