czworokąt wpisany w okrąg
Kamilo_7: Bok AB czworokąta ABCD wpisanego w okrąg jest średnicą tego okręgu. W punkcie D poprowadzono
styczną l do tego okręgu, która tworzy z bokami AD i DC kąty ostre odpowiednio o miarach 20
stopni i 30 stopni. Oblicz miary kątów wewnętrznych czworokąta ABCD.
11 lis 20:11
Janek191:
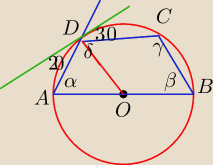
Mamy
δ = 180
o − ( 20 + 30)
o = 130
o
więc
β = 180
o − δ = 180
o − 130
o = 50
o
I ∡ ADO I = I ∡ DAO I bo Δ ADO jest równoramienny,
więc
α = I DAO I = I ADO I = 90
o − 20
o = 70
o
więc
γ = 180
o − α = 180
o − 70
o = 110
o
Odp. α = 70
o, β = 50
o, γ = 110
o, δ = 130
o
==========================================
Czworokąt ABCD jest wpisany w okrąg, więc α + γ = β + δ = 180
o
Styczna do okręgu jest prostopadła do odcinka DO.
11 lis 21:11
Janek191:
Mamy
δ = 180
o − ( 20 + 30)
o = 130
o
więc
β = 180
o − δ = 180
o − 130
o = 50
o
I ∡ ADO I = I ∡ DAO I bo Δ ADO jest równoramienny,
więc
α = I DAO I = I ADO I = 90
o − 20
o = 70
o
więc
γ = 180
o − α = 180
o − 70
o = 110
o
Odp. α = 70
o, β = 50
o, γ = 110
o, δ = 130
o
==========================================
Czworokąt ABCD jest wpisany w okrąg, więc α + γ = β + δ = 180
o
Styczna do okręgu jest prostopadła do odcinka DO.
11 lis 21:11
Eta:
I znów te "klony"
11 lis 21:23
Janek191:
Można usuwać niepotrzebnych bliźniaków
11 lis 21:25
Eta:
Hehe
takie ładne rysunki
Kto nie zobaczy na pierwszym? to może ujrzy na drugim?
11 lis 21:28