Zadania różne: okrąg, równania, nierówności, zadanie z treścią Patii568: 1. Przez punkt leżący na zewnątrz okręgu poprowadzono dwie styczne do tego okręgu. Punkt styczności podzieliły okrąg na dwa łuki 2:7 . Miara kąta rozwartego utworzonego przez te styczne jest równa A.100° B.120° C.140° D.160° 2.Ile punktów wspólnych mają okręgi x²+(y−1)²=4 i (x−4)²+(y−4)²=9 A.0 B.1 C.2 D.3 3.Odległość punktu P(−3,2) od prostej y=−2x+1 jest równa: A.5 B.3 C. √5 D. √13 4. Odległość na osi liczbowej między pierwiastkami równania 2+x−x²=0 wynosi: A.0 B.1 C.2 D.3 5.Rozwiąż równanie x³−7x²−3x+21=0 6.Rozwiąż nierówności: a) 3x²−10x+3≥0 b) |2x+12|≥ 10 7.Liczby : x−3, 2x, 5x+18 są kolejnymi wyrazami ciągu geometrycznego. Wyznacz x. 8.Wykresem funkcji kwadratowej y=¹₂ x²+bx+c jest parabola o wierzchołku W(−4,−1). Oblicz b i c. 10. W czasie wakacji Marcin przejechał rowerem ze stałą prędkością odległość z miasteczka A do B licząca 120km. Gdyby jechał ze średnią prędkością o 5 km/h większą to przejechałby tę odległość w czasie o 2h krótszym. Wyznacz średnią rzeczywistą prędkość Marcina i rzeczywisty czas przejazdu. BARDZO PILNE! PROSZĘ O DOKŁADNE OBLICZENIA.

Hajtowy: Zadanie 5 x(x²−3)−7(x²−3)=0 (x−7)(x²−3)=0 x=7 v x=√3 v x=−√3 Zadanie 6 a) 3x²−10x+3≥0 Δ=100−36=64 √Δ=8

	10−8		1
x1=		=
	6		3

	18
x2=		=3
	6

	1
x ∊ (−oo;		> ∪ <3;+oo)
	3

Hajtowy: Zadanie 3 P(−3,2) ⇒ (x₀;y₀) y=−2x+1⇒ 2x+y−1=0 Odległość punktu P(−3;2) od prostej o równaniu Ax+By+C=0 jest dana wzorem:

|Ax0+By0+C|
√A2+B2

Podstaw i wylicz

Hajtowy: Zadanie 3

|5|		5
	=		=√5
√5		√5

Odp. C

Hajtowy: 2.Ile punktów wspólnych mają okręgi x²+(y−1)²=4 i (x−4)²+(y−4)²=9 Zielony okrąg S₁=(0;1) r₁=2 Czerwony okrąg S₂=(4;4) r₂=3 Jak widać na załączonym obrazku, mają 2 pkt wspólne. Odp. C

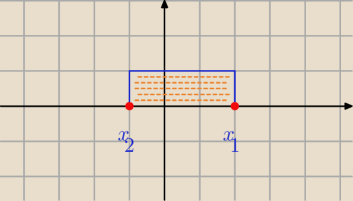
Hajtowy: 4. Odległość na osi liczbowej między pierwiastkami równania 2+x−x²=0 wynosi: −x²+x+2 = 0 Δ=9 √Δ=3

	−1−3
x1=		=2
	−2

	−1+3
x2=		=−1
	−2

Jak widać na załączonym obrazku Odp. D

Hajtowy:

	1
8.Wykresem funkcji kwadratowej y=		x2+bx+c jest parabola o wierzchołku
	2

W(−4,−1). Oblicz b i c. Postać kanoniczna funkcji kwadratowej: y=a(x−p)²+q Gdzie p, q − współrzędne wierzchołka [W(p,q)]

	1
Wiemy, że a=
	2

Podstawiając do wzoru:

	1
y=		(x+4)2+1
	2

By dowiedzieć się jaką wartość mają współczynniki b i c należy z postaci kanonicznej przejść do ogólnej rozwiązując odpowiednie działania:

	1
y=		(x+4)2+1
	2

1
	(x2+8x+16)+1=0
2

1
	(x2+8x+17)=0
2

x²+8x+17=0 b=8 c=17

Hajtowy: Więcej mi się nie chce Zrób coś sam