tyronometria
lina: Wiedząc, ze sinα kąta ostrego jest rowny √8√15 4,
oblicz wartość wyrażenia (sinα+cosα)2
10 lis 21:53
lina: wiem, ze (sinα+cosα)2 = 1−2sinαcosα
wiem także, że sin2α+cos2α=1
zatem skoro znam sinα
mogę obliczyć cos2α w następujący sposób: 1−sin2α=cos2α
ale co dalej? i jak to wygląda pod podstawieniu liczb?
10 lis 21:57
lina: mam tak:
1− (√8√154)2 = cos2α
1− 8+√1516=cos2α
co dalej?
10 lis 21:59
lina: ?
10 lis 22:01
lina: :(
10 lis 22:05
lina: ....
10 lis 22:26
katarzynka:
10 lis 22:35
Eta:
| √8√15 | | √8*3,9 | |
| ≈ |
| ≈U{√31{4} >1 |
| 4 | | 4 | |
0<sinα<1
zatem taki kąt α −− nie istnieje
Napisz poprawną treść zadania!
10 lis 22:37
katarzynka: | | √8+√15 | |
poprawka: ma być |
| |
| | 4 | |
10 lis 22:41
katarzynka: ?
10 lis 22:42
linia: tak, tyle, ze pierwiastek z 15 jest dodany pod dużym pierwiastkiem z 8
10 lis 22:43
10 lis 22:46
lina: ech, ktoś znalazł podobne zadanka, a tresci tez do konca nie zna
mój błąd
10 lis 22:50
lina: Eta jakbyś mogła pomóc − bardzo wdzięczna będę!
10 lis 22:50
lina: 
10 lis 22:57
Eta:
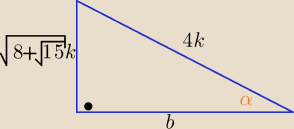
k>0
b
2= (4k)
2−(
√8+√15 k)
2 = 16k
2−(8+
√15)k
2
b
2= 16k
2−8k
2−
√15k
2= 8k
2−
√15k
2
b=
√8−√15 k
| | √8+√15 | | √8−√15 | |
(sinα+cosα)2= 1−2sinα*cosα= 1−2* |
| * |
| =........ |
| | 4 | | 4 | |
teraz dokończ......
10 lis 22:58
Eta:
I co? dokończone?
| | 1 | | 1 | | 1 | | 1 | |
...= 1− |
| √(8−√15)(8−√15)= 1− |
| *√64−15= 1− |
| *7 = |
| |
| | 8 | | 8 | | 8 | | 8 | |
10 lis 23:08
lina: tak, dziękuję bardzo!
10 lis 23:19