wyznaczanie dziedziny funkcji abecadło: Potrzebuje pomocy, nie wiem jak to ruszyć Wyznacz dziedzinę następujących funkcji: a) log_2x+3(2^x − 8) i b) log_4−x(x² − 1)

Dorota: trzeba wyjść od podstaw logarytmów − log_ab gdzie a>0 i a≠1 b>0 czyli trzeba znaleźć te zależności w rozwiązaniu układów nierówności a) 2x+3>0 2^x−8>0 z założeniem,że 2x+3≠1 tak samo drugie myślę,ze sobie poradzisz

Dorota: właściwie to nie jest układ nierówności, tylko trzeba by znaleźć część wspólną zbiorów rozwiązań pierwszej i drugiej nierówności, z wyłaczeniem,że 2x+3≠1

Dorota: 2x+3>0 − dziedzina to x >−³₂ czyli x⊂(−³₂,+∞) oraz 2x+3≠1 czyli x≠−1 oraz 2^x>8 czyli 2^x>2³ czyli x>3 ⇒x⊂(3,+∞) x spełniające te trzy warunki znajdują się w przedziale (czyli to jest dziedzina) x⊂(3,+∞)

Bogdan: Dzień dobry. Witam Doroto. Jak nazwać wyrażenie: 2x + 3 ≠ 0. Czy jest nierówność ? Bo równością na pewno nie jest. Można je zapisać tak: 2x + 3 < 0 i 2x + 3 > 0. Jest to więc, jak widać nierówność. Określając dziedzinę podanych w zadaniach wyrażeń, rozwiązujemy układ nierówności.

Bogdan: Poprawiam nieścisłość: 2x + 3 < 0 lub 2x + 3 > 0 (lub, nie i )

Dorota: Dzień dobry. Bogdanie jak zwykle racja − zawęziłam pole poszukiwań. Skoro w pierwszej wyszło,że x>−³₂ i jednocześnie musi być różne od 1 ( ≠) nie zajmowałam się już przedziałem poniżej 1. Druga nierówność x>3 wyjaśniła mi to jednoznacznie. czyli metoda nieprecyzyjna a wynik prawidłowy?

Bogdan: Nie analizowałem Twojego rozwiązania, chodziło mi w mojej wypowiedzi o uznanie wyrażenia 2x + 3 ≠ 0 i tego typu wyrażeń za nierówność.

Dorota: ile to człowiek zapomniał już z tej szkoły, bardzo dziękuję za cenne rady

Bogdan: 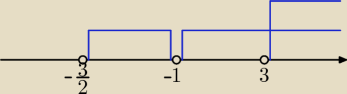Doroto, Twoje rozwiązanie jest jak najbardziej prawidłowe, x ∊ (3, +∞). Proponuję stosować w takim zapisie znak ∊, a nie znak ⊂

Dorota: właśnie nie mogłam znaleźć odpowiedniego znaczka − dziękuję.