Oblicz pole ograniczone wykresami funkcji Potrzebująca pomocy: Czy ktoś pomoże mi to rozwiązać? Proszę. 1Oblicz pole ograniczone wykresami funkcji: y=x² − 9, y= −x² + 3x 2 napisz równanie paraboli mając jej ognisko : F(2,3) i kierownice: x−8=0 3 Dana jest funkcja y = −2x³ − x² a)wyznacz przedziały monotoniczności i ekstrema funkcji b) napisać równanie stycznej do wykresu funkcji w punkcie P(1,−3)

duduś: Bogdan z pewnością pomoże

Bogdan: Pomogę, jeśli zmienisz nick na swoje imię

duduś: Klara ..........

AS: Zadanie 1 1. Ustalam granice całkowania − rozwiązując układ równań y = x² − 9 , y = −x² + 3*x ⇒ x² − 9 = −x² + 3*x ⇒ 2*x² − 3*x − 9 = 0 Rozwiązaniem tego równania: x1 = −1.5 , x2 = 3 Są to granice całkowania 2.Ponieważ obszary które nas interesują znajdują się nad i pod osią Ox trzeba by dzielić na trzy obszary i każdy z nich osobno obliczać. Dlatego korzystniej jest przesunąć cały obszar całkowania do góry o 10 j wtedy pole szukane się nie zmieni a wszystkie obszary będą dodatnie Po dodaniu do obu funkcji 10 j otrzymuję równania y = x² + 1 v = −x² + 3*x + 10 3. Szukane pole 3 3 S = |[(−x² + 3*x + 10) − (x² + 1)]dx = |(−2*x² + 3*x + 9)dx = −1.5 −1.5

−2*x3		3*x2
	+		+ 9*x | 3 =
3		2

−1.5

−2		3		−2		−3		3		−3		−3
	*33 +		*32 + 9*3 − (		*(		)3 +		*(		)2 + 9*		=
3		2		3		2		2		2		2

	27		2		27		3		9		27		61
−18 +		+ 27 −		*		−		*		+		=
	2		3		8		2		4		2		2

Odp. Pole szukanego obszaru wynosi 61/2 j²

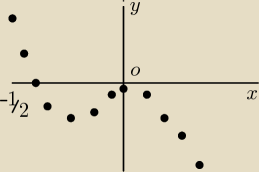
AS: Zadanie 3 Dana funkcja y = −2*x³ − x² = −x²*(2*x + 1) Miejsca zerowe: − 1/2 i 0 (pierwiastek podwójny) Pochodna funkcji y' = −6*x² − 2*x = −2*x*(3*x + 1) Miejsca zerowe pochodnej: −1/3 − 0 Badam znak pochodnej w przedziałach: (−∞,−1/3) , (−1/3,0) , (0,∞) przedział dla x −∞ −1/3 0 ∞ znak pochodnej funkcji ++++++ 0 − − − − − 0 ++++++++ wartość funkcji −1/27 0 Pochodna w punkcie x = −1/3 zmienia znak z + na − oznacza to,że w tym punkcie występuje minimum.Wynosi ono −1/27 Pochodna w punkcie x = 0 zmienia znak z − na + oznacza to,że w tym punkcie występuje maksimum.Wynosi ono 0 Równanie stycznej y − yo = f'(xo)*(x − xo) xo = 1 , yo = −3 , f(x) = −6*x² − 2*x f(xo) = −6*1² − 2*1 = −8 Równanie stycznej y − (−3) = −8*(x − 1) ⇒ y + 3 = −8*x + 8 ⇒ y = −8*x + 5 Równanie stycznej: y = −8*x + 5

AS: Zadanie 2 Parabola jest to m.g. punktów,równo oddalonych od kierownicy i ogniska. Stąd równanie: V(x − 2)² + (y − 3)² = 8 − x | stronami do kwadratu x² − 4*x + 4 + (y − 3)² = 64 − 16*x + x² (y − 3)² = −12*x + 60 Szukane równanie paraboli: (y − 3)² = −12*x + 60

Bogdan: Witaj Asie. W zadaniu 2 otrzymałem podobne rozwiązanie, ale w niektórych miejscach mam inne znaki.

AS: No oczywiście paskud chochlik dał o sobie znać − niech go licho spali. Dziękuję za poprawkę Poprawiam przedział −∞ −1/3 0 ∞ znak pochodnej funkcji − − − − − − 0 + + + + + + 0 − − − − − − ↘ ↗ ↘ Pochodna w punkcie x = −1/3 zmienia znak z − na + oznacza to,że w tym punkcie występuje minimum.Wynosi ono −1/27 Pochodna w punkcie x = 0 zmienia znak z + na − oznacza to, że w tym punkcie występuje maksimum.Wynosi ono 0

Bogdan: Asie, mówiłem o zadaniu z parabolą

Bogdan: A chochlików też nie lubię, chociaż i mnie się czasami czepiają

AS: Drogi Bogdanie , oświeć mnie ,bo nie widzę błędu. Serdeczne pozdrowienia.

Bogdan: Asie, otrzymałem równanie paraboli: (y − 3)² = 12(x − 5), sprawdź moje rozwiązanie, może to ja gdzieś pomieszałem znaki i teraz chochlik puszcza do mnie oko

AS: Bogdanie Sporządziłem wykres Twojej i mojej krzywej.Biorąc pod uwagę rozmieszczenie ogniska i kierownicy ramiona powinny być skierowane w lewą stronę i tak jest u mnie. Niestety u Ciebie są zwrócone w prawą stronę a więc niezgodnie z położeniem ogniska i kierownicy. Parabola przecina kierownicę.

Bogdan: No i chochlik mnie złapał. Masz Asie oczywiście rację. Dziękuje za sprawdzenie i pozdrawiam.

AS: Uff jaka ulga.

Ice: W zadaniu pierwszym z wykresami, w obliczeniach pola wystapil blad... Liczac tak jak podał Bogdan, Wynik nie jest równy 61/2 a 243/4... Chociaz sposob liczenia i tak jest dziwny...