W urnie znajduje się n kul. Yoshik: W urnie znajduje się n kul, z których 6 jest czerwonych. Jakie powinno być n, aby przy losowaniu dwóch kul bez odkładania ich do urny prawdopodobieństwo wylosowania dwóch kul czerwonych było większe od 1/3.

Yoshik: Robię zadania z drzewa i dochodzę do 30/n²−n > 1/3 Liczę z tego deltę, ale wychodzi n1 = −9 n2=10 a w odpowiedziach jest nE {6,7,8,9} Help...

Maslanek:

	n 2
|Ω|=

	6 2
|A| =

	1
P(A)≥		, prawda?
	3

Założenie n≥6 (to całkiem logiczne )

Maslanek: Nierówność ma być ostra, więc:

	1
P(A)>
	3

Eta: |Ω|= n*n=n² |A|= 6*6= 36 ( dwie czerwone)

	1
P(A) >
	3

	36		1
rozwiąż równanie		>
	n2		3

Maslanek: Eto, bez odkładania

Eta: Ajjjjjjjjjjjjjjjj mea culpa ( "bez odkładania ich do urny" −−− muszę założyć okulary !

Yoshik:

	n 2
|Ω|=		jak to rozpisać ?

Yoshik:

	n 2		n!
|Ω|=		=		ale jak dalej
			(n−2)!*2!

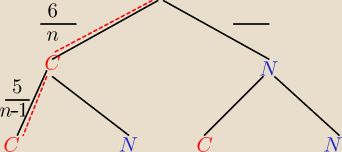
Mila: n≥6

	6		5		30
P(CC)=		*		=
	n		n−1		n*(n−1)

30		1
	>		/*(n−1)*n
n*(n−1)		3

	1
30>		*(n−1)*n /*3
	3

90>n²−n n²−n−90<0 i n∊N₊ i n≥6 Δ=1+360=361

	1−19		1+19
n1=		=−9 lu n2=		=10
	2		2

n∊(−9,10) i n∊N₊ i n≥6 n∊{6,7,8,9}

Yoshik: Dzięki Ci wielkie

Eta: