/ Piotr 10: Dwie koszule męskie można włożyć do trzech róźnych szuflad. Na ile sposobów można było to zrobić? Wyszło mi, że na 6 sposobów

123: podejmujesz 2 deczje 1 na 3 sposoby i 2 na 2 sposoby (szuflady) 3x2= 6

Saizou : a nie 3*3=9 bo I II III 1,2 − − 1 2 − 1 − 2 2 1 − 2 − 1 − 2,1 − − 1 2 − 2 1 − − 2,1 oraz pierwszą koszulę możemy wpakować do 1,2,3 szuflady czyli 3 sposoby drugą koszulę tak samo czyli 3 możliwości 3*3=9

Piotr 10: Nie wiem, ja i tak nie ogarniam tego : /

Krzysiek: Nie jest napisane 2 różne koszule, więc (1,−,2) to to samo co (2,−,1)

Saizou : ale szuflady są rozróżnialne, czyli to chyba ma znaczenie

Eta: 2 koszule → 3 szuflad : 3²=9 sposobów

Krzysiek: no ok, ale jeżeli w I i III szufladzie będzie koszula to przecież nie ma znaczenia która koszula będzie w której szufladzie bo są takie same. więc rozmieszczenie: 1 − 2 jest takie samo jak: 2 − 1 Przyjmując,że koszule są takie same.

Maslanek: Ale koszule nie Więc kombinacje + przypadki, gdy wkładamy koszule do jednej szuflady. Albo: kombinacje z powtórzeniami ewentualnie (tego nigdy nie sotosowałem, ale wydaje się dobre )

Saizou : mniej więcej to łapię, tylko kto normalny będzie się zastanawiał na ile sposób można rozłożyć koszulę w szufladach najlepiej powiesić na wieszak

Piotr 10: Masakra... Ja to idę, siedzę na tym działem od 18 i nic nie rozumiem : /

Saizou : don't worry be happy You'll understand it, I'm sure

Eta:

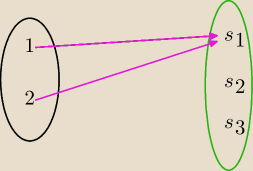
Mila: Piotrze, tu masz do czynienia z funkcjami {k1,k2} argumenty {s1,s2,s3] wartości, ktore możesz wybrać 1) f(k1)=s1 f(k2)=s1 (s1,s1) obydwie do 1 szuflady 2) f(k1)=s2 f(k2)=s2 (s2,s2) obydwie do 2 szuflady 3) f(k1)=s3 f(k2)=s3 (s3,s3) Teraz do różnych (s1,s2)(s2,s3)(s1,s3)(s3,s1)(s2,s3)( (s3,s2) Zapis (s1,s2) oznacza pierwsza koszula do 1 szuflady, druga do drugiej. Masz ciągi dwuwyrazowe z 3 elementów, n^k n− liczba elementów ( szuflad do których wrzucamy), k − liczba przedmiotów. ( z góry wrzucamy).

Krzysiek: Mila,Eta ale Wy rozróżniacie koszule a przecież równie dobrze można zrobić dla nierozróżnialnych. W tekście jest wyraźnie napisane "różnych szuflad" więc równie dobrze napisaliby "różne koszule".

Saizou : czyli że mamy I II III 11 − − 1 1 − 1 − 1 − 11 − − 1 1 − − 11 inne możliwości to powtórzenia

	3!
czyli inaczej mówić wariacja bez powtórzeń V23=		=6
	(3−1)

dobrze myślę

Eta: @ Krzysiek Jeżeli masz wrzucić koszule do trzech szuflad, to jestem przekonana,że wrzucisz wszystkie : ( w paski, kropki) do pierwszej z brzegu ( nawet nie będziesz ich ogladał

Maslanek:

	3 2
Kombinacja bez powtórzeń:		i dwie koszule w każdej z trzech: zatem 3 mozliwości

Razem 3+3=6.

Mila: Może i tak, Krzysiu. Ja nie kupuję mężowi jednakowych, ale zawsze różne i dlatego taki sposób.

Eta:

Krzysiek: A ja nie piszę,że oczywiste jest że koszule się różnią ale chodzi o rozwiązanie matematyczne I wydaje mi się,że powinniśmy rozpatrywać nierozróżnialne koszule

Mila: 1) wersja Na ile sposobów można umieścić w 3 szufladach 2 koszule tak, aby każda była w innej szufladzie? 3*2=6

PW: Znowu autor zadania dał nam "zagadkę myślową". Szuflady są "różne", a koszule "męskie". Gdyby koszule były "damskie", wątpliwości by nie było − kobiety nie kupują jednakowych ubrań. Dlatego stoję na stanowisku, że koszule według autora są nierozróżnialne. Każda wersja rozwiązania jest dobra, byle wyraźnie napisać jakie założenie przyjęliśmy. Mam nadzieję, że ten autor nie formułuje zadań maturalnych.