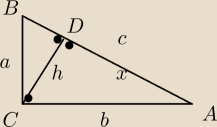
 Dane sa:
P(ADC)=54 i P(DBC)=96 (nieproporcjonalnie na rysunku, przepraszam)
Oblicz dlugosci wszystkich bokow w tym trojkacie (a, b, x, c−x)
Na razie doszedlem do tego, ze k=4/3 (pierwiastek z 96/64).
x*h/2=54 i (c−x)*h/2=96
Co dalej z tym zrobic?
Dane sa:
P(ADC)=54 i P(DBC)=96 (nieproporcjonalnie na rysunku, przepraszam)
Oblicz dlugosci wszystkich bokow w tym trojkacie (a, b, x, c−x)
Na razie doszedlem do tego, ze k=4/3 (pierwiastek z 96/64).
x*h/2=54 i (c−x)*h/2=96
Co dalej z tym zrobic?
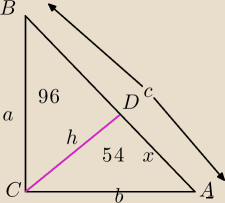 54+96=150
54+96=150
| b | ||
ΔADC∼ΔCDB w skali | ||
| a |
| b | 54 | |||
( | )2= | ⇔ | ||
| a | 96 |
| b | 3 | 3 | ||||
k= | = | ⇔4b=3a⇔b= | a | |||
| a | 4 | 4 |
| 1 | ||
PΔABC= | a*b=150⇔ | |
| 2 |
| 3 | ||
a* | a=300 | |
| 4 |
| 3 | ||
b= | *20=15 | |
| 4 |
| 1 | |
*c*h=150 | |
| 2 |
 bo też już miałam pisać rozwiązanie
bo też już miałam pisać rozwiązanie 
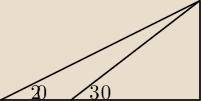 Dzieki za pomoc. Mam jeszcze jedno zadanie za ktore nie wiem jak sie zabrac.
Łódka zbliża się do mostu ze stałą prędkością. W pewnym momencie z łódki widać most pod kątem
20°. Po upływie 10minut widać go pod kątem 30°. Po jakim czasie od tej chwili łódka dopłynie
do mostu?
Dzieki za pomoc. Mam jeszcze jedno zadanie za ktore nie wiem jak sie zabrac.
Łódka zbliża się do mostu ze stałą prędkością. W pewnym momencie z łódki widać most pod kątem
20°. Po upływie 10minut widać go pod kątem 30°. Po jakim czasie od tej chwili łódka dopłynie
do mostu?
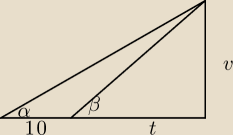 α=200, β=300
α=200, β=300
| t | t | |||
ctgβ= | ⇒v= | |||
| v | ctgβ |
| t+10 | t+10 | |||
ctgα= | ⇒v= | |||
| v | ctgα |
| t | t+10 | ||
= | |||
| ctgβ | ctgα |