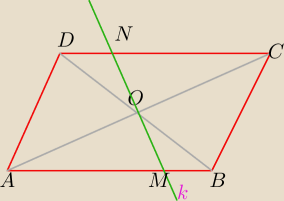
. Piotr 10: Przez środek symetrii O równoległoboku ABCD poprowadzono prostą k, która podzieliła ten równoległobok na dwa czworokąty: AMND oraz MBCN. Wykaż, że pola czworokąta AMND i MBCN są równe. IADI=ICBI INMI jest wspólną długością boku obu czworokątów IAMI=INCI ⋀ IDNI=IMBI gdyż dowolnie poprowadzona prosta przez środek symetrii dzieli te dwa boki na 4 cztery części. Odpowiednie części równoległych boków równoległoboku są sobie równe. A więc czworokąt AMND jest przystający do czworokąta MBCN □AMDN ≡ □ MBCN Dobrze czy nie ?

Piotr 10: ⇔P₁=P₂ zapomniałem tego dopisać

Piotr: To jak

Piotr 10:

krystek: Wykazałabym z przystawanaia Δ równośc boków DN i MB

Piotr 10: A czy mój dowód jest poprawny, czy muszę wykazać jeszcze coś ?

krystek: Nie znam tw o podziale na który się powołujesz.

Piotr 10: Sam to wymyśliłem, narysowałem sporo takich prostych przechodzące przez środek symetrii i zawsze ten podział jest spełniony

Mila: Punkt O jest środkiem symetrii równoległoboku⇒MO=ON, AO=OC i ∡NOC≡∡AOM na podstawie cechy bkb mamy: ΔNOC≡ΔAOM⇒NC=AM Ponadto : DN=MB Trapezy MBCN,AMND maja równe pola.

Piotr 10: Mila czyli mój dowód jest do poprawy, tak?

Piotr 10: ?

Mila: Tam nie masz dokładnie wyjaśnionego dlaczego odpowiednie odcinki są równe, zrobiłam to sugerowała Krystek.

Piotr 10: OK dziękuję