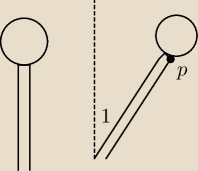
Zadanie z trygonometrii Student: Mam prośbę. Muszę obliczyć zmianę siły nacisku kuli o pormieniu R (głowy) na rurkę (kręgosłup) po otchyleniu ciała o 1 stopień w miejscu gdzie będzie największa. Podejzewam że będzie to pkt na obwodzie kręgosłupa (P). Promień kręgosłupa wynosi ok 2 cm. Proszę o pomoc, muszę zamieścić dane w referacie z medycyny. Z góry dziękuję. Z liceum pamiętam że można to zrobić funkcjami trygonometrycznymi cos x = √Q{N} alw wydaje mi się że jest to obliczenie dla środnka ciężkości. Mi chodzi o największą wartość siły nacisku.

Student: ^Q_N *

MQ: Skoro układ jest stabilny, to jak równoważony jest moment skręcający.

Student: Mógłbyś bardziej wytłumaczyć? Jestem na medykuz liczbami nie miałem już długo styczności.

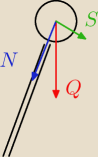
MQ: Co ci równoważy S?

Student: Nie mam pojęcia. Pamiętam z trygonometri że są zależności między S,N i Q. Z fizy zawsze byłem noga a tu przyszło mi się zmierzyć. Mógłbym jeszcze jedną podpowiedź? Albo jakiś wzór? Potzrebuje procentów o ile się zwiększy nacisk. W najdalszym punkcie.

MQ: Człowieku! Jak ci mamy pomóc, jak ty nie wiesz, jaka jest geometria problemu. 1. Jak ta głowa jest trzymana na kijku? 2. W których miejscach przytrzymywana? 3. Czy są jakieś więzy? Skoro nie spada, to siła S^→ musi być jakoś równoważona −− jakieś wiązadła? Nie wiem −− nie jestem medykiem.

Zadanie: Tak są, przepraszam za mało danych. Głowa na kijku ma być symulacją zmiany sił działających na kręgosłup przy odchyleniu ciała o 1 stopień. Między głową a kręgosłupem są więzadła które równoważą siłę S. Pt\rzytrzymywana w każdym miejscu równomiernie. Jeżeli potrzebne jeszcze jakieś dane to powiedz. Ja próbowałem tak : Q=mq(siła nacisku w pionie) Nacisk po odchyleniu to 1/cos 1. Ale wydaje mi się że to w środku ciężkości. Mi chodzi o pkt w którym ta siła jest największa. Da się to zrobić?

MQ: Kręgosłup traktujemy jako pustą w środku rurkę −− ciężar rozkłada się po obwodzie? Jaką jest symulowana średnica głowy?

Student: Rurka pełna, średnica głowy 20 cm. (Jeżeli nie da się z pełną obliczyć, poprosiłbym z pustą)

MQ: Na kiedy to masz mieć?

Wazyl: Jutro wieczór

Student : Jutro do 18

Wazyl: Coś mi wskoczyło w komputer i nicki mi zmienia

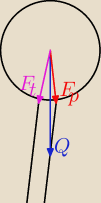
MQ: No to rychło wczas się do tego zabrałeś. Na dzisiaj mogę ci rozpatrzyć tylko przypadek dwuwymiarowy (przekrój naszego przypadku), czyli głowa w kształcie dysku podparta dwoma prętami. Ciężar głowy Q rozkłada się na dwie siły F_p i F_t. Głowa przechylona jest w stronę F_p. r −− promień kręgosłupa = 2cm R −− promień głowy = 10cm przy głowie prostej kąt pomiędzy siłami nacisku na obwód a siła ciężkości wynosi

	r
α=arcsin
	R

Przy przechyle o kąt β, kąt pomiędzy Q a F_p wynosi α−β, a pomiędzy Q a F_t wynosi α+β Dalsza część w następnym poście.

Student: Jak Ci dziękować?

MQ: Mamy równoległobok sił i z niego wynikają następujące zależności: Q=F_pcos(α−β)+F_tcos(α+β) oraz F_psin(α−β)=F_tsin(α+β) wyliczam z drugiego F_t i wstawiam do pierwszego:

	sin(α−β)
Ft=Fp
	sin(α+β)

	sin(α−β)		sin(α−β)
Q=Fpcos(α−β)+Fp		cos(α+β)=Fp*(cos(α−β)+		cos(α+β))
	sin(α+β)		sin(α+β)

Stąd wyliczamy F_p

	sin(α−β)
Fp=Q/(cos(α−β)+		cos(α+β))
	sin(α+β)

F_p −− siła nacisku do przodu −− największa. Problem 3−wymiarowy wymaga rozpatrzenia nacisku rozłożonego liniowo po obwodzie rurki, a to wymaga już większego namysłu. Dzisiaj nie dam już rady, bo jutro wstaję o 5:45

Student: Dziękuję bardzo. Jeżeli uda Ci sie przedstawić to w 3wymiarze będzie super. Jak skontaktować się z Tobą prywatnie w ramch jakichś podziękować? Ratujesz mnie!

MQ: Jutro, jeśli coś wymyślę, to dorzucę tu po południu jakieś rozwiązanie, ale wątpię, czy w tak krótkim czasie mi się coś uda −− trochę za późno. Teraz się już wyłączam.