Nierówności wielomianowe Kamix: Witam Jak rozwiązać nierówność tego typu? (3x³+x²−8x+4)(−2x²−3x−8)>0 Mnożyć nawiasy przez siebie chyba nie bardzo mi się opłaca, bo dostanę wielomian stopnia 5... Czy muszę w takim przypadku rozpatrzyć dwa przypadki, że: 3x³+x²−8x+4>0 ⋁ −2x²−3x−8>0 i znaleźć pierwiastki za pomocą twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych? Czy jest inna, szybsza metoda?

Saizou : zapoznaj się z tym https://matematykaszkolna.pl/strona/142.html

Kamix: Saizou, teorię jako tako znam, lecz nie pomogło mi to bardzo, bo w tym przykładzie jakoś ciężej odczytać pierwiastki i chodzi mi o to, czy zastosować tutaj twierdzenie o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych czy też poleci to jakoś szybciej.

MathGym: dobrze myślisz tylko porównujesz do zera i szukasz pierwiastków, pierwszy wyłącz czynnik drugi człon z delty

Kamix: Problem jest taki, że pierwszego członu nie mogę wyłączyć czynnik, bo jest "goła" czwórka bez x, a w drugim delta wychodzi ujemna, czyli nie ma pierwiastków Czyli jak na mój gust 1 leci z twierdzenia i tyle

MathGym: jesteś poziom podstawowy czy rozszerzony pierwszy podziel wielomian przez x−1 da się

Kamix: Poziom rozszerzony Ale żeby podzielić wielomian przez dwumian (x−1) muszę być pewny, że 1 jest pierwiastkiem tego wielomianu... A skąd mam to wiedzieć przystępując do rozwiązywania?

Hajtowy: Pomagam, chwilka

MathGym: = (x−1)(3x²+4x−4)

	2
x = 1 v x = −2 v x =
	3

rozwiązanie

	2
x∊(−∞, −2) u (		,1)
	3

MathGym: policz ze W(1) = 0 a to jest pierwiastek

MathGym: i jak załapałeś/aś

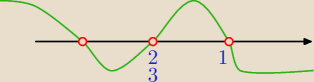
Hajtowy: (3x³+x²−8x+4) W(1)=0 3 1 −8 4 1 3 4 −4 3 4 −4 0 (3x²+4x−4)(x−1)(−2x²−3x−8)>0 (3x²+4x−4) Δ=16+48 = 64 √Δ=8

	−4−8		−12
x1=		=		=−2
	6		6

	−4+8		4		2
x2=		=		=
	6		6		3

(−2x²−3x−8) Δ=9−64 < 0

	2
(x+2)(x−		)(x−1)(−2x2−3x−8) > 0
	3

	2
x=−2 v x=		v x=1
	3

	2
Odp. x ∊ (−oo;−2) ∪ (		;1)
	3

Mila: Nie wymnażasz , lecz rozkładasz na czynniki liniowe, o ile się da. 1) P(x)=(3x³+x²−8x+4) 2) q(x)=(−2x²−3x−8) tu sprawa prosta ,Δ=9−4*(−2)*(−8)=9−64<0 trójmian przyjmuje tylko wartości ujemne (a=−2<0) Stąd nierówność:(3x³+x²−8x+4)(−2x²−3x−8)>0 jest równoważna nierówności (3x³+x²−8x+4)<0 Ad1)P(x)=(3x³+x²−8x+4)<0 szukamy miejsca zerowego wśród liczb

	2
{+1,−1,+2,−2,+4,−4,		,.itd..}
	3

P(1)=3+1−8+4=0 Schemat Hornera x=1 3 1 −8 4 3 4 −4 0 Mamy nierówność: (x−1)*(3x²+4x−4)<0 dalej już sam rozwiąż Napisz odpowiedź.

Hajtowy: Kamix... (3x³+x²−8x+4) => Podstaw x=1 i sprawdź czy wyjdzie Ci zero

Kamix: Okey, ale skąd niby ma mi przyjść do głowy że akurat W(1)=0... Równie dobrze mógłbym przyjąć, że W(2)=0, co nie byłoby prawdą, że W(3)=0, także nie byłoby prawdą. Według mnie wynika to z twierdzenia o pierwiastkach wymiernych, sprawdzam, która z liczb {−1−¹₃,−²₃,−2,−4,−⁴₃,1,¹₃,2,²₃,4,⁴₃, zeruje mi wielomian, i z tego odczytałbym, że W(1) ale sprawdzenia pozostałych liczb zajęłoby mi spoooooro czasu

Rodney: Jeśli chodzi o pierwszy nawias, czyli 3x³+x²−8x+4, to korzystamy z tego, że jak suma współczynników jest równa 0, to 1 jest rozwiązaniem wielomianu Twoje współczynniki tutaj to: 3, 1, −8, 4 3+1−8+4=0, więc Wielomian taki dzieli się przez wielomian x−1 Podziel i będziesz miał już potem w nawiasach tylko wielomiany stopnia drugiego, a z tym powinieneś sobie spokojnie radzić

Kamix: Widzę, że wszyscy się opieracie na schemacie Hornera. Problem w tym, że nigdy nie miałem z nim styczności, nie obowiązuje on w liceum, przynajmniej mnie, mimo profilu matematycznego o nim nie uczyli... Czyli dla mnie pozostaje tylko twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych i ta żmudna praca sprawdzania każdej z liczb czy wyzeruje wielomian?

Hajtowy: Kamix, musisz sprawdzać lub jak się da to grupować (bo jest prościej) Najpierw się sprawdza najbardziej prawdopodobne (policzyć w głowie można, że W(1) = 0 ) Chyba,, że Twój mózg jeszcze tak dobrze nie funkcjonuje, to kalkulator w dłoń i liczyć

Kamix: O Rodney, bardzo dobra metoda z tymi współczynnikami, nie miałem o niej pojęcia a widzę, że jest przydatna

pomocy: sprawdzasz dzielniki wyrazu wolnego w tym przypadku 4

Kamix: Hahaha, Hajtowy, co do obliczania w pamięci wartości wielomianu dla 1 czy 2, w tym przypadku nawet 3 nie byłoby problemu, gorzej z ułamkami typu ²₃ itp.

Mila: Kamix, schemat Hornera stosujesz do dzielenia, gdy juz znasz pierwiastek. Możesz dzielic zwyczajnie, pisemnie. Pokazałam Ci jak sprawdzasz czy liczba jest pierwiastkiem. Zwykle przykłady są tak dobrane, że szybko znajduje się pierwiastek.

Hajtowy: To jest taki zwykły sposób "na lekcji" −−−−−−−−−−−−−−−−−−−− (3x³+x²−8x+4):(x−1)=3x²+4x−4 −3x³+3x² −−−−−−−−−−−−−−−−− 0 ...... 4x²−8x −4x²+4x −−−−−−−−−−−−−−−−−−−− −4x+4 4x − 4 −−−−−−−−−−−−−−−−−−− 0 0

Kamix: Oczywiście dzielenia wielomianu tradycyjną metodą mam opanowane bardzo dobrze, także nie ma z tym problemu ; ) Dziękuję Wam wszystkim za pomoc !