funkcja wymierna
Radek:
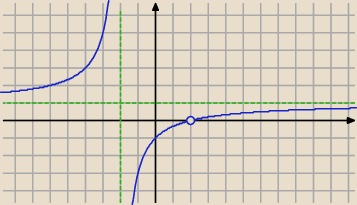
Podaj dziedzinę wyrażenia i sprowadź do najprostszej postaci U{x
2−4x+4{x
2−4}
D=R\{−2.2}
| (x−2)2 | | x−2 | |
| = |
| |
| (x−2)(x+2) | | x+2 | |
dobrze myślę ?
6 lis 18:25
MathGym: OK
6 lis 18:30
Radek:
A może ktoś inny jeszcze się wypowie
?
6 lis 18:33
Radek: ?
6 lis 19:12
Hajtowy: Bardzo pięknie
6 lis 19:13
Ratarcia: jest poprawnie
6 lis 19:14
Mila:
Może napisz postać kanoniczną funkcji:
6 lis 19:14
MathGym: Radek: Dziękuje za zaufanie
6 lis 19:16
Radek:
@MathGym przepraszam ale bardzo rzadko jesteś na forum więc wolę żeby ktoś potwierdził
?
6 lis 19:18
Radek: ?
6 lis 19:37
5-latek: Radek radze CI uwazac. A co bedzie jak [MathGym]] to
Eta 
Ona tak czesto zmienia nicki . Wczoraj np byla
Jula
6 lis 19:42
Radek:
Wiem ,że wczoraj Pani Eta była Jula ale @MathGym to inna osoba
6 lis 19:43
Mila:
Radek Dobrze.
Tak właśnie jest 5− latku. Pozdrawiam.
6 lis 19:46
Eta:
6 lis 19:48
Radek:
| | x+3 | |
Mam pytanie czemu dla prostych funkcji np |
| nie ma takich kółeczek ? |
| | x−2 | |
6 lis 19:49
Mila:
Bo w x=2 jest asymptota pionowa , a pozostałe liczby należą do dziedziny.\
6 lis 19:51
Radek:
Czyli takie kółeczka są tylko jak mam bardziej skomplikowaną funkcje i ją upraszczam ?
6 lis 19:52
5-latek: Pozdrawiam
Milu 
Siedze teraz w domu i sie lecze .
6 lis 19:53
Radek: ?
6 lis 20:05
MathGym: MathGym to zawsze MathGym − nie wiem w jakim celu ludzie zmieniają nicki
6 lis 20:07
Radek:
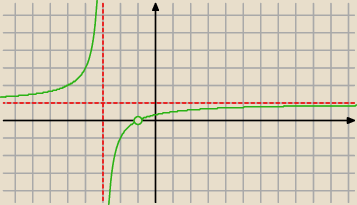
| | x2+2x+1 | |
określ dziedzinę wyrażenia i naszkicuj wykres funkcji f(x)= |
| |
| | x2+4x+3 | |
| (x+1)2 | | x+1 | |
| = |
| |
| (x+1)(x+3 | | x+3 | |
ok ?
6 lis 21:18
Mila:
Radek, dobrze.
5−latek, to przykre, życzę zdrówka.,kwiatek>
MathGym, chyba dla urozmaicenia .
6 lis 21:26
Radek:
| | |x2−1| | |
A jak mam taką funkcję |
| |
| | x3−x | |
x
3−x≠0
x(x
2−1)≠0
x(x−1)(x+1)≠0
D=R\{−1.0.1}
i w jakich przedziałach ją rysuje
(−
∞,−1)
<−1,1)
<1,
∞) ?
6 lis 21:31
Mila:
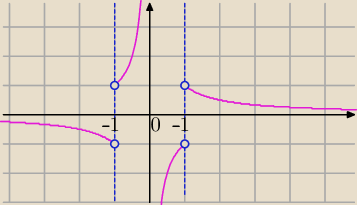
Popatrz na dziedzinę. przedziały otwarte.
Rozpisz wzór funkcji po uproszczeniu.
6 lis 21:52
Radek:
Ale w każdym z tych przedziałów wartość w module będzie dodatnia ?
6 lis 21:54
Radek:
| | x2+2x+1 | |
A jeszcze do zadania 21:18 Uzasadnij, że zbiorem wartości funkcji f(x)= |
| |
| | x2+4x+3 | |
jesr zbiór R\{0,1}
Więc ZW=R\{1} a skąd to 0 ?
6 lis 22:01
Mila:
21:28
dla x=−1 nie istnieje wartość funkcji:
| | x+1 | |
ale dla g(x)= |
| mamy g(−1)=0 i musimy pamiętac o funkcji f(x) z której wyłoniła się |
| | x+3 | |
g(x).
6 lis 22:06
Radek:
Czyli prawidłowo trzeba do g(x) podstawić −3,−1 bo te argumenty nie należą do dziedziny ?
6 lis 22:11
Mila:
Masz podstawić te, które należą do dziedziny g(x) a nie należą do dziedziny f(x).
6 lis 22:14
Radek:
dla f(−1) mam 0 8 to nie należy do zbioru wartości bo kółeczko niezamalowane ?
6 lis 22:15
Radek:
Wiem, że zadaje dużo pytań ale mam jeszcze jedno:
Dlaczego podstawiamy te które należą do g(x) a nie należą do f(x) ? z czego to wynika ?
6 lis 22:18
Mila:
Przecież (−3) nie możesz wstawic do wzoru g(x) bo otrzymasz zero w mianowniku, a (−1) możesz
podstawić do g(x) , ale nie możesz do f(x).
6 lis 22:25
Radek: ale podstawiając a=−1 dla g(x) otrzymam jakąś konkretną wartość ?
6 lis 22:26
Radek: Już nie musi Pani tłumaczyć zrozumiałem
Ale teraz odnośnie tego zadania 21:31?
6 lis 22:30
Mila:
Masz rysunek 21:52, ale prosiłam o rozpisanie wzoru funkcji. Umiesz, czy mam Ci to pokazać?
6 lis 23:03
Radek:
A post 21:54 ?
6 lis 23:33
Mila:
Jutro Ci to rozpiszę, dobranoc.
6 lis 23:56
Radek:
7 lis 19:26
Radek: ?
7 lis 20:56
Radek: ?
7 lis 21:34
Mila: JUż jestem tu.
7 lis 21:40
Mila:
D: x≠1,x≠−1 ,x≠0
1) |x
2−1|=x
2−1 ⇔x
2−1>0 ⇔x<−1 lub x>1
wtedy
| | x2−1 | | x2−1 | | 1 | |
f(x)= |
| = |
| = |
| |
| | x3−x | | x(x2−1) | | x | |
2) |x
2−1|=−(x
2−1) dla x∊(−1,1)
wtedy:
| | −(x2−1) | | −1 | |
f(x)= |
| = |
| |
| | x*(x2−1) | | x | |
rysunek Ci zrobiłam 21:52
Czy wszystko tu jasne?
7 lis 21:47
Radek:
To może Pani odpowiedzieć na pytanie 21:54 ?
7 lis 21:48
Radek:
puk−puk...
7 lis 22:21
Eta:
znów dzięcioł ?
7 lis 22:28
Radek:
Chodzi o mój post 21:48 ?
7 lis 22:28
Radek: ?
7 lis 23:05
Mila: 21:48 nie ma postu.
9 lis 19:51
Radek: Ale w każdym z tych przedziałów wartość w module będzie dodatnia ?
9 lis 20:00
Mila:
Tak, ale f(x) nie , bo mianownik nie jest w module.
9 lis 20:25