stereometria-przekrój płaszczyzną
adam: czy mógłby mi ktoś pomóc w tym zadaniu?
Krawędź podstawy graniastosłupa czworokątnego prawidłowego ma długość 4, a krawędź boczna
długość 3
√2 Oblicz pole przekroju tego graniastosłupa płaszczyzną wyznaczoną przez przekątną
graniastosłupa i środek krawędzi bocznej zawartej w prostej skośnej do prostej zawierającej tę
przekątną.
Chodzi mi tylko o to gdzie jest ten środek

Ciężko mi to zauważyć na rysunku. Z resztą już
sobie poradzę
6 lis 11:26
Bizon:
czytaj raz jeszcze to zadanko ... czytaj aż zrozumiesz −

Gdzie jest środek krawędzi wiadomo ... pytanie jest której ...
Powodzenia −

6 lis 11:37
adam:
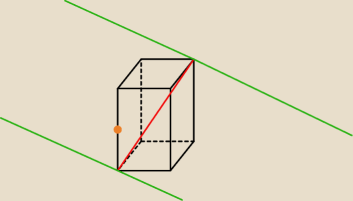
jeśli czerwona linia to przekątna graniastosłupa i zielone wyznaczają płaszczyznę, w której
jest zawarta to wydaje mi się że ten punkt będzie tam gdzie wskazałem
6 lis 11:51
Bizon:
... przekątna płaszczyzny nie wyznacza ... jako ze prosta może wyznaczać jedynie
pęk płaszczyzn. Dopiero prosta i punkt wyznaczają płaszczyznę.
Ale krawędź wybrałeś dobrze −

6 lis 12:06
Bizon:
... przepraszam ... krawędź nie ta −:(
6 lis 12:26
Bizon:
prosta zawierająca tą krawędź na której zaznaczyłeś punkt nie jest skośna do prostej
zawierającej przekątną graniastosłupa jako, że przecinają się w wierzchołku graniastosłupa
6 lis 12:30
adam:
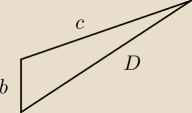
chyba muszę jednak prosić o dalszą pomoc.
Wyliczyłem boki tego trójkąta i wyszły odpowiednio:
D(przekątna graniastosłupa)=
√50
b=
12H=
3√22
c=
√36,5
Ze wzoru Herona, ciężko było by to liczyć, jest jakiś inny sposób?
6 lis 12:40
Bizon:
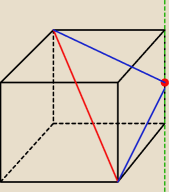
6 lis 12:50
adam: czyli zostają tylko te dwie krawędzie? jak liczyłem z pole z krawędzią na prawo od punktu to
wynik się nie zgadzał, a przy tej drugiej krawędzi wynik pozostanie taki sam, i nie pasuje do
odpowiedzi − wynosi 20
już naprawdę nie wiem jak to zrobić

6 lis 12:51
irena_1:
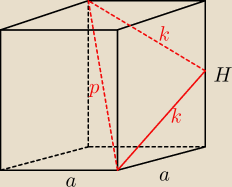
p
2=4
2+4
2+(3
√2)
2=16+16+18=50
p=5
√2
| | 3√2 | | 18 | | 82 | |
k2=( |
| )2+42= |
| +16= |
| |
| | 2 | | 4 | | 4 | |
Przekrój to trójkąt równoramienny
h− wysokość opuszczona na podstawę p
h=2
√2
6 lis 12:59
adam: Też mi tyle wyszło, ale odpowiedź z tyłu książki wynosi 20. Nie wiem czy oni się pomylili, czy
może chodzi jednak o ten inny punkt.
6 lis 13:11
irena_1:
Nazwij dolną podstawę ABCD, a górną odpowiednio EFGH.
Przekątna prostopadłościanu to prosta BH. Krawędzie boczne skośne z tą przekątną to AE oraz CG.
Proste skośne nie mają wspólnych punktów. Na pewno więc nie chodzi o tamten punkt (na pierwszym
rysunku Adama). Bo przekątna i krawędź maja wspólny wierzchołek podstawy.
6 lis 13:25
Adam: Ale ta płaszczyzna zależy od tego którą przekątną weźmiemy. Niemniej jednak wynik wychodzi taki
sam 10. To chyba jednak jest błąd w odpowiedziach. Dziękuje Wam za pomoc.

6 lis 15:10
 Ciężko mi to zauważyć na rysunku. Z resztą już
sobie poradzę
Ciężko mi to zauważyć na rysunku. Z resztą już
sobie poradzę
 Gdzie jest środek krawędzi wiadomo ... pytanie jest której ...
Powodzenia −
Gdzie jest środek krawędzi wiadomo ... pytanie jest której ...
Powodzenia −
 jeśli czerwona linia to przekątna graniastosłupa i zielone wyznaczają płaszczyznę, w której
jest zawarta to wydaje mi się że ten punkt będzie tam gdzie wskazałem
jeśli czerwona linia to przekątna graniastosłupa i zielone wyznaczają płaszczyznę, w której
jest zawarta to wydaje mi się że ten punkt będzie tam gdzie wskazałem

 chyba muszę jednak prosić o dalszą pomoc.
Wyliczyłem boki tego trójkąta i wyszły odpowiednio:
D(przekątna graniastosłupa)=√50
b=12H=3√22
c=√36,5
Ze wzoru Herona, ciężko było by to liczyć, jest jakiś inny sposób?
chyba muszę jednak prosić o dalszą pomoc.
Wyliczyłem boki tego trójkąta i wyszły odpowiednio:
D(przekątna graniastosłupa)=√50
b=12H=3√22
c=√36,5
Ze wzoru Herona, ciężko było by to liczyć, jest jakiś inny sposób?


 p2=42+42+(3√2)2=16+16+18=50
p=5√2
p2=42+42+(3√2)2=16+16+18=50
p=5√2
