:) ICSP: Dla jakich wartości parametru k równanie

log(xk)
	= 2
log(x+1)

ma tylko jeden pierwiastek ?

Piotr 10: xk > 0⇔ x > 0 ⋀ k > 0 v x <0 ⋀ k<0 x+1 > 0⇔x > −1 Czyli k >0 log(x+1)≠0 10⁰≠x+1 1≠x+1 x≠0 log(xk)=2log(x+1) log(xk)=log(x+1)² kx=x²+2x+1 x²+(2−k)x+1=0 Δ=4−4k+k²−4=k²−4k=0 ⇔ k(k−4)=0 ⇔ k=0 v k=4 k=4 ale nie wiem czy to dobrze

Jula: Ok k=4

Mila: Niezupełnie, jeszcze dla k<0.

ZKS: Należałoby jeszcze rozpatrzyć Δ > 0 i kiedy x₁ ∊ D_f oraz x₂ ∉ D_f.

ICSP: Właśnie dziwne to zadanie Dziedzina ma trzy założenia : 1^o kx > 0 2^o x > −1 3^o x ≠ 0 Dalej rozwiązując dochodzimy do : x² + (2 − k)x + 1 = 0 Δ = k² − 4k Gdy Δ = 0 dostajemy dla k = 0 sprzeczność oraz dla k = 4 x = −1 Więc k = 4 spełnia warunki zadania Zostaje tylko przypadek gdy Δ > 0 i nie mam pomysłu jak go rozpatrzyć

Saizou : czyżby wystarczył tylko warunek że Δ>0 i f(−1)<0

ICSP: x musi być tego samego znaku co k K jest dodatnie więc x również musi być dodatnie Δ > 0 i f(0) < 0 ?

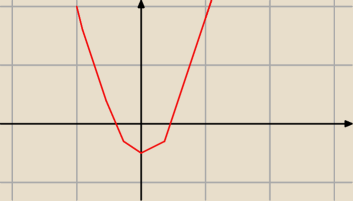
Saizou : dla czegoś takiego co narysowałem będą 2 rozwiązania jeśli dobrze myślę , a spełnia to założenie że f(0)<0

Godzio:

log(xk)
	= 2
log(x + 1)

x > − 1 oraz xk > 0 ⇒ x ∊ (−1,0) i k < 0 lub x > 0 i k > 0 1^o k < 0 ⇒ x ∊ (−1,0) log(xk) = log(x + 1)² xk = x² + 2x + 1 x² + x(2 − k) + 1 = 0 Jeden pierwiastek należący do przedziału (−1,0) 1^o Δ = 4 − 4k + k² − 4 = k² − 4k = 0 ⇔ k = 0 lub k = 4, (k = 0 odpada) Dla k = 4

	2
x0 =		= 1 ∉ (−1,0)
	2

2^o Δ > 0 ⇒ k ∊ (−∞,0) U (4,∞) f(−1) * f(0) < 0 ⇒ k * 1 < 0 ⇒ k < 0 2^o x > 0 i k > 0 x² + x(2 − k) + 1 = 0 1^o Δ = 0 ⇒ k = 4 ⇒ x = 1 pasuje 2^o Δ > 0 i f(0) < 0 ⇒ sprzeczność Odp: k ∊ (−∞.0) U {4}

Godzio: Nie zwróciłem uwagi: 1^o k < 0 więc Δ = 0 nie trzeba badać bo k = 4 też tego nie spełnia

ICSP: Dziękuje wszystkim

Mila: Właśnie skończyłam oglądać film i miałam pisać, ale Godzio był szybszy.