Funkcja wymierna Radek:

	16
Na podstawie wykresu funkcji f(x)=		rozwiąż nierówność f(x)≤8
	x

16
	≤8 x≠0
x

16≤8x −8x≤−16 x≥2 x∊<2,∞) w odpowiedziach (−∞,−2>suma(0,∞) ? Jeśli by rozwiązać nierówność wymierną to tak wyjdzie bo 0 Nie należy do D więc będzie otwarty ale czemu moim sposobem nie wychodzi ?

Piotr 10: Nie możesz pomnożyć przez x

Piotr 10: Przypuśćmy, że x<0, czyli , np. −3 wtedy byś musiał zmienić znak

Radek: razy x² ?

Radek: Nigdy nie można mnożyć razy x ?

Piotr 10:

16
	− 8 ≤ 0
x

16−8x
	≤ 0 ( mnożę obustronnie przez kwadrat mianownika,jest on zawsze dodatni)
x

(16−8x)x ≤0 dziach (−∞,−2>∪ (0,∞) Zera nie bierzemy , bo nie należy do dziedziny

Piotr 10: Jeżeli byśmy mieli podane w poleceniu, że x∊R₊, to wtedy możemy mnożyć przez x, bo wiemy że jest dodatni

Radek: Rozwiązując nierówność wymierną też mi wyszło Dzięki za odpowiedź

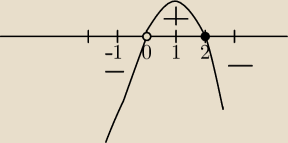
Mila: Masz odczytac z wykresu. Jeśli chcesz rozwiąząc algebraicznie to np.tak: 1)

16
	−8≤0 i x≠0
x

16−8x
	≤0 możemy zbadać znak iloczynu
x

(16−8x)*x≤0⇔ 8(2−x)*x≤0 x<0 lub x>2 2) albo tak, x≠0

16
	≤8 /*x2
x

16x≤8x² 8x²−16≥0 8x(x−2)≥0⇔x<0 lub x>2

Mila: Skąd macie (−2)? Dwa razy się pomyliłam?

Piotr 10: Mila jest ok, ja się pomyliłem