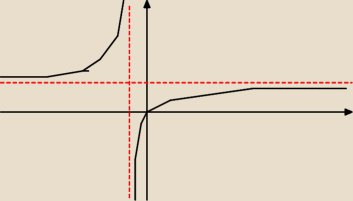
Naszkicuj wykres funkcji f, wajdzik: Naszkicuj wykres funkcji f, która każdej wartości parametru m przyporządkowuje sumę dwóch pierwiastków równania (m+1)x²−3mx+m+1=0 f(m)=m₁+m₂

	3m
f(m)=		, gdzie m≠1
	m+1

	2
D:m∊(−∞,−		)U(2,+∞)
	5

Powstaje taki wykres: I nie rozumiem skąd pojawiają się tutaj te asymptoty oraz wykresy. Za pomocą tabelki mogę do tego pomału dojść ale to nie zmienia faktu, że tego nie rozumiem. Mógłby mi ktoś to wytłumaczyć

wajdzik: m≠−1

Mila: (m+1)x²−3mx+m+1=0 1) m+1≠0, aby mieć równanie kwadratowe. 2) równanie kwadratowe ma dwa różne pierwiastki⇔Δ>0 Δ=9m²−4*(m+1)*(m+1)=5m²−8m−4 5m²−8m−4>0⇔

	2
m∊(−∞,−		)U(2,+∞)
	5

	−b
3) x1+x2=		⇔
	a

	3m
x1+x2=
	m+1

	3m
f(m)=		(funkcja homograficzna)
	m+1

przekształcamy wzór do postaci kanonicznej

	3m+3−3		3*(m+1)		−3
f(m)=		=		+
	m+1		m+1		m+1

	−3
f(m)=		+3
	m+1

	−3
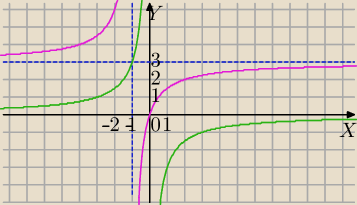
5) Rysujemy wykres funkcji g(m)=		zielony wykres
	m

6) przesuwamy wykres g(m) o wektor [−1,3] otrzymujemy wykres

	−3
f(m)=		+3
	m+1

wajdzik: Dzięki Milu, jak przekształcałem do postaci kanonicznej to mi wyszło totalnie inaczej, dziwne

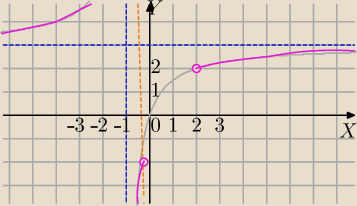Mila: To było wyjaśnienie do wykresu funkcji:

	−3
f(m)=3+		dla m∊R\{−1}
	m+1

	−2
Wykres f(m) dla m∊(−∞,−1)∪(−1,		)∪(2,∞)
	5

Mila: Napisz swoje obliczenia to Ci coś podpowiem.