przeksztalcenia zadanie: 1. Korzystajac z definicji przeksztalcen, lecz bez uzywania ich wzorow, znajdz obrazy punktu A(2,−5) przez: a) jednokladnosc o srodku S(1, 3) i skali k=3 wektor SA'=k*wektor SA [x'−1;y'−3]=3[1,−8] A'(4,−21)

	1
b)powinowactwo prostokatne o osi x=2 i skali k=−
	2

o osi x=2, czyli P(2,0) wektor PA'=k*wektor PA

	1
[x'−2;y'−0]=−		[2−2,−5−0]
	2

	5
A'(2,		)
	2

c) symetrie osiowa wzgledem prostej y=−1 P(2,−1) wektor PA'=−wektor PA [x'−2,y'+1]=−[0,−4] A'(2,3) d) symetrie srodkowa wzgledem punktu S(−3,2) wektor SA'=−wektorSA [x'+3,y'−2]=−[2+3,−7] A'(−8,9)

zadanie: 2.7. Poslugujac sie wzorami uzasadnij, ze zlozenie dowolnych dwoch translacji jest translacja. O jaki wektor? T₁: x'=x+a oraz T₂: x'=x+c y'=y+b y'=y+d a, b wspl. pierwszego wektora, c,d wspl. drugiego wektora T₂◯T₁=T₂(T₁)=T₂(x+a, y+b)=(x+a+c, y+b+d) x'=x+a+c y'=y+b+d; jest to translacja o wektor [a+c, b+d] T₁◯T₂=T₁(T₂)=T₁(x+c, y+d)=(x+c+a, y+d+b) czyli jest to translacja o wektor [c+a, d+b] czyli bez wzgledu na to jak zlozymy 2 translacje bedzie to translacja o ten sam wektor.

zadanie: 3.Czy istnieje translacja, ktora punkt A(1,2) przenosi na punkt A'(3,4), zas punkt B(−1,0) na B'(−1,0)? Odpowiedz uzasadnij. A(1,2), A'(3,4) x'=x+a y'=y+b czyli a=3−1=2 b=4−2=2 wektor [2,2] B(0,1), B'(−1,0) x'=x+c y'=y+d czyli c=−1 d=−1 wektor [−1,−1] Nie istnieje, bo wektory przy obu translacjach musza byc takie same.

zadanie: 4. Napisz rownanie pewnej elipsy a nastepnie znajdz rownanie jej obrazu przez obrot o kat

	π		π
		oraz −		.
	6		4

Ze wzoru na obrot x'=xcosα−ysinα y'=xsinα+ycosα przeksztalcenie odwrotne do obrotu o kat α jest obrotem o kat −α, czyli x=x'cosα+y'sinα y=−x'sinα+y'cosα

	π
dla α=
	6

	√3		1
x=		x'+		y'
	2		2

	1		√3
y=−		x'+		y'
	2		2

	x2		y2
wybrana elipsa:		+		=1
	4		9

podstawiajac mam:

√3   1   ( x'+ y')2   2   2		1   √3   (− x'+ y')2   2   2
	+		=1
4		9

34x'2+√32x'y'+14y'2		34y'−√32x'y'+14x'2
	+		=1 /*36
4		9

	3		√3		1		3		√3		1
9({		x'2+		x'y'+		y'2)+4({		y'−		x'y'+		x'2)=36
	4		2		4		4		2		4

bede pisac bez primow

27		9√3		9
	x2+		xy+		y2+3y2−2√3xy+x2=36 /*4
4		2		4

27x²+18√3xy+9y²+12y²−8√3xy+4x²=144

	π
31x2+10√3xy+21y2=144 rownanie elipsy przez obrot
	6

zadanie:

	π
a przez obrot o kat −		to tez podkladam do tego wzoru po przeksztalceniu odwrotnym tzn,
	4

	π
do tego samego wzoru co o kat		tak?
	6

zadanie:

	π
5. Dana jest krzywa x2+xy+y2−1=0. Obroc ja o kat		(wszystko jedna w ktora strone) i
	4

wtedy rozstrzygnij co to za krzywa. czyli ze wzoru juz tego drugiego po przeksztalceniu mam:

	√2		√2
x=		x'+		y'
	2		2

	√2		√2
y=−		x'+		y'
	2		2

podstawiajac do wzoru mam:

	√2		√2		√2		√2
(		x'+		y')2+(		x'+		y')*
	2		2		2		2

	√2		√2		√2		√2
(−		x'+		y')+(−		x'+		y')2−1=0
	2		2		2		2

2x²+2y²−2x²+2y²+2y²+2x²−4=0 2x²+6y²−4=0 /:2 x²+3y²=2

x2		y2
	+		=1 jest to elipsa
2		23

zadanie: prosilbym o sprawdzenie i jezeli to mozliwe o poprawienie bledow

Mila: Zadanie 1 dobrze, jeszcze sprawdzę powinowactwo, ale chyba dobrze. 2) dobrze 3) czy B i B' maja takie same współrzędne? W treści inaczej niż w rozwiązaniu. Rozwiązane dobrze dla B(0,1), B'(−1,0) 4) dobrze. lepiej będzie sie liczyć, gdy skorzystasz z wzorów :

	1
x=		*(√3x'+y')
	2

	1
y=		(−x'+√3y)
	2

5) dobrze łatwiej gdy podstawisz wzory

	1
x=		*(x'+y.)
	√2

	1
y=		*(y'−x'))
	√2

6) 15:58 tak.

zadanie: dziekuje bardzo

Mila: Jak leci? Widzę,że się rozkręcasz.

zadanie: Uzasadnij bezposrednio z definicji, ze przeksztalcenie zadane wzorem T(x, y)=(x−2y,−2x+4y+1) a) nie jest roznowartosciowe b) nie jest ''na'' nie potrafie tego zrobic moglbym prosic o pomoc?

zadanie: ?

Mila: a) T(x,y)=(x−2y,−2x+4y+1)⇔ T(x,y)=(x−2y, −2(x−2y)+1) Jeżeli będziemy przekształcać punkty płaszczyzny P(2a,a) , to obrazem będzie punkt (0,1) czyli dla P₁(2a,a) i P₂(2b,b), gdzie a≠b Mamy: T(2a,a)=(2a−2a,−2*2a+4a+1)=(0,1) T(2b,b)=(2b−2b,−2*2b+4b+1)=(0,1) Zapisz to wg schematu z wykładu.

zadanie: dziekuje

zadanie: przeksztalceniem odwrotnym do powinowactwa prostokatnego o osi L i skali k jest powinowactwo

	1
prostokatne o osi L i skali		prawda?
	k

zadanie: Na przykładzie jednokładności i przesunięcia pokaż, że składanie przekształceń nie jest na ogół przemienne. Wylicz, że oba złożenia są jednokładnościami, znajdując ich skale i środki. Czy się różnią? T₁: x'=k(x−s_x)+s_x oraz T₂: x'=x+a y'=k(y−s_y)+s_y y'=y+b T₂◯T₁=T₂(k(x−s_x)+s_x, k(y−s_y)+s_y)=(k(x−s_x)+s_x+a, k(y−s_y)+s_y+b) jest to jednokladnosc o skali k a jak obliczyc srodek?

zadanie: ?

zadanie: 6. Sprawdź, że pole każdego trójkąta pod wpływem powinowactwa prostokątnego o skali k zmienia się w stosunku |k|. 7. Wyprowadź wzór rzutu prostokątnego P na prostą −2x+3y−5=0 a następnie sprawdż za pomocą wyliczenia, że P◯P=P. Uzasadnij geometrycznie tą zależność dla dowolnego rzutu. 8. a)Znajdz rownnaie parametryczne obrazu prostej x=2t−3 ,y=−3t przez przeksztalcenie T(x,y)=(x+2y ,y+3).b)Poslugujac sie rownaniami parametryczny,i uzasadnij ze obrazem dowolnej prostej przez to przeksztalcenie jest prosta.c)Zrob to samo co w b) posugujac sie rownaniami ogolnymi. 9. Sprawdz poslugujac sie a)rownaniem parametrycznym prostej b)rownaniem ogolnym ze obrazem dowolnej prostej przez jednokladnosc jest zawsze prosta do niej rownolegla. moglbym prosic o jakies wskazowki do tych zadan?

zadanie: 10. wylicz, ze zlozeniem symetrii srodkowych wzgledem punktow S₁ i S₂ jest przesuniecie o wektor 2*S₁S₂. A(x,y) S₁(a,b) S₂(c,d) T₁: S₁A'=−S₁A oraz T₂: S₂A'=−S₂A T₂◯T₁=.... dobrze mysle?

Mila: Ad. 20:58, zrób drugie złożenie. Poszukam w teorii.

zadanie: drugie zlozenie T₁◯T₂=T₁(x+a, y+b)=(k(x+a−s_x)+s_x, k(y+b−s_y)+s_y)

zadanie: ja juz ide spac dobranoc

Mila: 19:38 Dobrze. Złożenie dwóch powinowactw prostkątnych o tej samej osi i stosunkach(skalach) k i m jest powinowactem prostokatnym o skali k*m. 6) Oblicz pole Δ o wierzchołkach: A(x₁,y₁),B(x₂,y₂), C(x₃,y₃) wg wzoru

1
	|det(AB→,AC→) |następnie oblicz pole ΔA'B'C' , obierz skalę k.
2

7) już robiliśmy podobne 8)

Mila: srodek nowej jednokładności: S(m,n) SP'^→=k*SP^→, chociaż chyba można z wzorów pokombinować.

Mila: 20:58 jutro Ci napiszę, bo sporo pisania , a już idę spać. Wiem, jak Ci wyjaśnić.

zadanie: 6)powinowactwo wzgledem osi x A(x₁,y₁),B(x₂,y₂), C(x₃,y₃) A'(x₁,ky₁),B'(x₂,ky₂), C'(x₃,ky₃) AB=[x₂−x₁, y₂−y₁]; A'B'=[x₂−x₁, k(y₂−y₁)] AC=[x₃−x₁, y₃−y₁]; A'C'=[x₃−x₁, k(y₃−y₁)]

	1
PΔABC=		I(x2−x1)(y3−y1)−(y2−y1)(x3−x1)I
	2

	1
PΔA'B'C'=		Ik((x2−x1)(y3−y1)−(y2−y1)(x3−x1))I
	2

czyli zmienia sie w stosunku IkI

Mila: 6) P_ΔA'B'C'=|k|*P_ΔABC Wniosek: Pole każdego trójkąta pod wpływem powinowactwa prostokątnego o skali k zmienia się w stosunku |k|.

zadanie: a do 23:52 jakies uwagi?

Mila: Składanie jednokładności i translacji: J=J_S^k: x'=k(x−s_x)+s_x oraz T: x'=x+a y'=k(y−s_y)+sy y'=y+b S(s_x,s_y) środek jednokładności o skali k. J◯T(x,y)=J(x+a,y+b)=[k*(x+a−s_x)+s_x,k(y+b−s_y)+s_y] J' nowa jednokładność o skali równej k SZukamy środka jednokładności J' S'=(m,n) P(x,y) dany punkt, P'(x',y') obraz punktu P w złożeniu przekształceń J◯T Z definicji jednokładności: S'P'^→=k*S'P^→ S'P'^→[x'−m, y'−n]=[k*(x+a−s_x)+s_x−m,k(y+b−s_y)+s_y−n] S'P^→=[x−m,y−n] k*[x−m,y−n]=[k*(x+a−s_x)+s_x−m,k(y+b−s_y)+s_y−n]⇔ kx−km=kx+ka−ks_x+s_x−m i ky−kn=ky+kb−ks_y+s_y−n⇔ m−km=ka−ks_x +s_x i n−kn=kb−ks_y+s_y m(1−k)=ka+s_x*(1−k) i n(1−k)=kb+s_y*(1−k) / : (1−k) dla k=1

	k		k
m=		*a+sx i n=		+sy
	1−k		1−k

	k		k
S'(		*a+sx ,		+sy)
	1−k		1−k

1) Dla złożenia T◯J oblicz sam. 2) Zrób analizę złożenia , gdy k=1

zadanie: 8. x=2t−3=−3+2t y=−3t T(x,y)=(x+2y ,y+3) a) rownanie parametryczne obrazu prostej x=−3+2t+2(−3t)=−3+2t−6t=−3−4t y=−3t+3=3−3t b) dana prosta: przeksztalcenie: T(x,y)=(x+2y ,y+3) x=A_x+V_xt y=A_y+V_yt nowa prosta: x=A_x+V_xt+2(A_y+V_yt)=A_x+2A_y+2V_yt+V_xt y=A_y+V_yt+3=A_y+3+V_yt c) dana prosta: ax+by+c=0 a(x+2y)+b(y+3)+c=0 ax+2ay+by+3b+c=0 ax+(2a+b)y+3b+c=0 dobrze?

zadanie:

	k
w tej drugiej wspolrzednej srodka powinno byc chyba n=		*b+sy
	1−k

Mila: Zadanie 10) zrób, wykorzystując wzory na symetrie środkową ( to jest jednokladność o skali k=−1) Napisz .

Mila: 17:26, oczywiście, brakuje tam b, zwykła literówka. Jasne wyprowadzenie?

zadanie: wyprowadzenie jasne dziekuje 1) T◯J(x,y)=(k(x−s_x)+s_x+a, k(y−s_y)+s_y+b); S''(c, d)

	a−c		b−d
S''=(		+sx,		+sy)
	1−k		1−k

2) dla k=1 J_s¹: x'=x T: x'=x+a y'=y y'=y+b J◯T=(x+a, y+b) T◯J=(x+a, y+b) sa to translacje o wektor [a,b]

zadanie: 10) S(s_x, s_y) k=−1 x'=2s_x−x y'=2s_y−y S₁(s_x1, s_y1) S₂(s_x2, s_y2) A(x,y) A'(x',y') x'=2s_x1−x y'=2s_y1−y teraz: wsp. punktu A' podkladam do symetri wzgledem punktu S₂ i wyjdzie punkt A'' x''=2s_x2−2s_x1+x y''= 2s_y2−2s_y1+y ?

zadanie: a zadanie z 17:18 dobrze?

Mila: 10:07 Jeżeli S"(c,d) to nie możesz wyraz w zależności od c i d. Popraw.

zadanie: 9. a) rownanie parametryczne: jednokladnosc: x=A_x+v_xt x'=k(x−s_x)+s_x y=A_y+v_yt y'=k(y−s_y)+s_y x'=k(A_x+v_xt−s_x)+s_x=kA_x+kv_xt−ks_x+s_x=kA_x+(1−k)s_x+kv_xt y'=k(A_y+v_yt−s_y)+s_y=kA_y+kv_yt−ks_y+s_y=kA_y+(1−k)s_y+kv_yt b) rownanie ogolne ax+bx+c=0 a(k(x−s_x)+s_x))+b(k(y−s_y)+s_y))+c=0 dobrze?

zadanie:

	sx(1−k)+a		sy(1−k)+b
S''(		,		)
	2−k		2−k

zadanie: moglbym prosic o sprawdzenie tamtych zadan?

Mila: 10) 18:29 Dokończenie: x''=x+2(sx₂−sx₁) y''= y+2(sy₂−sy₁)⇔ Złożenie 2 symetrii środkowych .... jest translacją o wektor (2*S₁S₂)^→ 19:02 źle mianownik. Napisz co jeszcze sprawdzić, bo się pogubiłam. Sprawdzę później.

zadanie: 19:02 mianownik 1−k to a−c wyszlo dlatego bo ja przenoszac c z prawej strony na lewa i znowu przepisujac linijke napisalem c z prawej

zadanie: mam pytanie do zadania 10 to ostatecznie jaka jest odpowiedz?

zadanie: poprosilbym o sprawdzenie zadania 8 z 17:18 i zadania 9 z 18:49.

Mila: 10) Translacja o wektor 2*S₁S₂^→, coś jest niejasne?

Mila: 8)a) x=−3+2t y=0−3t u^→=[2,−3] −wektor kierunkowy T: x'=x+2y ⇔x=x'−2y y'=y+3⇔y=y'−3 x=x'−2*(y'−3)⇔ x=x'−2y'+6 y=y'−3 podstawiamy do równania prostej x'−2y'+6=−3+2t⇔x'=2y−9+2t y'−3=−3t⇔y'=3−3t x'=2*(3−3t)−9+2t⇔x'= 6−6t−9+2t⇔ x'=−3−4t y'=3−3t prosta v=[−4,−3] wektor kierunkowy prostej po przekształceniu b) nie wiem czy tak rozwiązywałeś x=a_x+u_xt y=a_y+u_yt u^→=[u_x,u_y] −wektor kierunkowy prostej T: x'=x+2y ⇔x=x'−2y⇔ x=x'−2y'+6 y=y'−3 x'−2y'+6=a_x+u_xt y'−3=a_y+u_yt x'=a_x+2a_y+(u_x+2u_y)*t y'=3+a_y+u_y*t x=a_x+2a_y+(u_x+2u_y)*t y=3+a_y+u_y*t − równanie prostej c) Ax+By+C=0 ogólne równanie prostej x=x'−2y'+6 y=y'−3 A(x'−2y'+6)+B(y'−3)+C=0 Ax'−2y'*A+6A+By'−3B+C=0 Ax'+(−2A+B)y'+6A−3B+C=0⇔ Ax+(−2A+B)y+6A−3B+C=0

Mila: 9) robię tą samą metodą.

zadanie: dziekuje ale to 9 zadanie co to znaczy ta sama metoda? tak jak w zadaniu 8 czy tak jak ja zrobilem ?(w co watpie) a to moje rozwiazanie poprawne jest?

Mila: Wyniki Twoją metodą są takie same. (9) rozwiązuje, moją metodą, jeśli było u Was na ćwiczeniach tak , jak Ty robisz, to dobrze. w 9b u Ciebie nie masz postaci z której widać, że prosta jest równoległa a to masz wykazać. Zaraz rozwiążę.

Mila: 9a) x=a_x+u_x*t y=a_y+u_y*t u→=[u_x,u_y] −wektor kierunkowy prostej J_S^k: S=(s_x,s_y) x'=k*(x−s_x)+s_x y'=k*(y−s_y)+s_y

	x'+k*sx−sx
x'=k*x−k*sx+sx ⇔x=
	k

	y'+k*sy−sy
y'=k*y−k*sy+sy ⇔y=
	k

x'+k*sx−sx
	=ax+ux*t ⇔x'+k*sx−sx=k*ax+k*ux*t
k

y'+k*sy−sy
	=ay+uy*t⇔y'+k*sy−sy=k*ay+k*uy*t
k

x'=s_x−k*s_x+k*a_x+k*u_x*t ⇔x'=k*a_x+s_x*(1−k)+k*u_x*t y'=−k*s_y+s_y+k*a_y+k*u_y*t⇔y'=k*a_y+s_y*(1−k)+k*u_y*t [ku_x,ku_y]=k*[u_x,u_y]⇔wektory kierunkowe prostych są równoległe⇔proste są równoległe.

Mila: b) m: A*x+B*y+C=0 równanie ogólne prostej J_S^k: S=(s_x,s_y)

	x'+k*sx−sx
x'=k*(x−sx)+sx⇔x=
	k

	y'+k*sy−sy
y'=k*(y−sy)+sy⇔y=
	k

	x'+k*sx−sx		y'+k*sy−sy
A*		+B*		+C=0 /*k
	k		k

A*(x'+k*sx−s_x)+B*(y'+k*sy−s_y)+C*k=0 A*x'+A*k*s_x−A*s_x+B*y'+B*k*s_y−B*s_y+C*k=0 A*x'+B*y'+(A*k*s_x−A*s_x+B*k*s_y−B*s_y+C*k)=0⇔ n: A*x+B*y+C₁=0 , C₁=(A*k*s_x−A*s_x+B*k*s_y−B*s_y+C*k) n||m

zadanie: dziekuje

zadanie: a jakas podpowiedz do 7?

Mila: podpowiedź 1. m: −2x+3y−5=0 − dana prosta P− dany punkt nie leżący na prostej m P' − rzut prostokątny, punktu P na prostą m, P'∊m i PP'⊥m Spróbuj samodzielnie popracować. Podpowiedź 2. Ax+By+C=0 równanie ogólne prostej Dla dowolnego D∊R prosta Bx−Ay+D=0 ( także −Bx+Ay+D=0) jest prostopadła do prostej Ax+By+C=0

Mila: To proste.

zadanie: wektor prostopadly do prostej m: [3,2] P(x, y) P'(x', y') x=x'−2t y=y'+3t podstawiam do rownania prostej m: −2(x'−2t)+b(y'+3t)−5=0 −2x'+4t+3y'+9t−5=0 13t=5+2x'−3y' /:13

	5+2x'−3y'
t=
	13

	5+2x'−3y'		9x'−10+6y'
x=x'−2*		=
	13		13

	5+2x'−3y'		4y'+6x'+15
y=y'+3*		=
	13		13

dobrze?

zadanie: ?

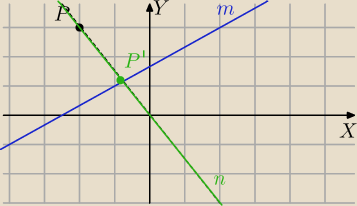
Mila: Na ogólnym równaniu prostych. P(p_x,p_y), P'(x',y') m: −2x+3y−5=0 i P'∊m n: 3x+2y+D=0 i P∊n⇔3*p_x+2p_y+D=0⇔D=−3*p_x−2p_y, n⊥m n: 3x+2y−3*p_x−2p_y=0 P' jest punktem przecięcia prostych m i n Rozwiązujemy układ równan −2x+3y−5=0 3x+2y−3*p_x−2p_y=0

	9*px+6*py−10
x=
	13

	6*px+4*py+15
y=
	13

Współrzędne rzutu prostokątnego punktu P(p_x,p_y) na prostą −2x+3y−5=0

	9*px+6*py−10
x'=
	13

	6*px+4*py+15
y'=
	13

Złożenie:

	9*px+6*py−10		6*px+4*py+15
P◯P(px,py)=P(		,		)=
	13		13

=.. dokończ na kartce, bo straszne piętrusy wychodzą

	9*px+6*py−10		6*px+4*py+15
=(		,		)=P(px,py)
	13		13

Geometryczne uzasadnienie :? Obrazem punktu P jest punkt P'∊m, obrazem punktu P'∊m w rzucie na prosta m jest ten sam punkt.

zadanie: dziekuje

Mila: