Permutacje Piotr 10: Przy okrągłym stole ustawiono 5 krzeseł. Na ile sposobów może usiąść 5 osób przy tym stole? Proszę o pomoc z wytłumaczeniem

Saizou : P₅=5!=120 bo −pierwszą osobę możemy posadzić na 1 z 5 krzeseł − drugą na 1 z4 krzeseł − trzecią na 1 z 3 krzeseł − czwartą na 1 z 2 krzeseł − piątą na 1 z 1 krzesła

Piotr 10: W odpowiedzi mam tak: 5!=120 ( uwzględniamy również miejsca zajmowane przez osoby przy okrągłym stole) 4!=24 ( uwzględniamy tylko rozmieszczenie osób względem siebie) Nie rozumiem tych odpowiedzi

Saizou : a to nie wiem, ja bym zrobił to tak jak napisałem powyżej, jeśli dobre rozumiem

Piotr 10: Cyfry 0,1,2,3,4,5,6 ustawmy losowo tworząc ciąg i potraktujmy go jako liczbę siedmiocyfrową której pierwszą cyfrą nie może być 0. Ile jest możliwych takich ustawień, w których otrzymamy liczbę siedmiocyfrową parzystą ? Ostatnia cyfra musi być postaci {0;2;4;6} ,a więc 4 sposoby Pierwsza cyfra 5 sposobów Druga cyfra 5 sposobów trzecia cyfra 4 sposoby czwarta cyfra 3 sposoby piata cyfra 2 sposoby szósta cyfra 1 sposób 4*5*5!=2400 co robię źle ?

Saizou : zakładam że liczby mogą się powtarzać! − czyli ostatnia (siódma) cyfra musi być {0,2,4,6} czyli 4 sposoby −na pierwszym miejscy nie może być 0, czyli mamy {1,2,3,4,5,6} czyli 6 sposobów − na drugim może być liczba ze zbioru {0,1,2,3,4,5,6} czyli 7 sposobów − na trzecim {0,1,2,3,4,5,6,} 7 sposobów − na czwartym {0,1,2,3,4,5,6} 7 sposobów − na piątym {0,1,2,3,4,5,6} 7 sposobów − na szóstym {0,1,2,3,4,5,6} 7 sposobów zatem 6*7*7*7*7*7*4=6*7⁵*4

Piotr 10: W odpowiedzi jest wynik: 6!+3*5*5!=2520

irena_1: Wracam do posadzenia osób przy stole − jeśli ważne jest, na którym krześle siedzi każda z osób, to takich usadzeń jest 5! (patrz wyjaśnienie Sazou) − jeśli ważne jest, kto siedzi koło kogo, to wszystkie ustawienia 5! trzeba podzielić przez 5 (bo identyczne są usadzenia 12345, 23451, 34512, 45123, 51234 i podobnie− inne).

	5!
Stąd		=4!
	5

Saizou : liczby nie mogą się powtarzać − 7 cyfra załóżmy że ostatnia to 0 czyli mamy 1 sposób − 1 cyfra liczby nie mają się powtarzać zatem mamy 6 opcji − 2 cyfra 5 sposobów − 3 cyfra 4 sposoby − 4 cyfra 3 sposoby − 5 cyfra 2 sposoby − 6 cyfra 1 sposób gdy na − 7 miejscy jest liczba ze zbioru {2,4,6} 3 sposoby − 1 cyfra 5 sposoby (bo bez 0 i ostatniej cyfry) − 2 cyfra 5 sposoby (bo tu już może być 0) − 3 cyfra 4 sposoby − 4 cyfra 3 sposoby − 5 cyfra 2 sposoby − cyfra 1 sposób ilość liczb: 1*6!+3*5*5! tak mi się wydaje

Piotr 10: Właśnie Saizou tak kombinowałem, że z tym zerem coś trzeba zrobić

irena_1: Jeśli pierwszą jest 1, 3 lub 5, to na końcu musi być 0, 2, 4 lub 6. Pozostałe 5 lokujemy dowolnie w środku. Mamy tutaj 3*4*5! Jeśli pierwsza to 2, 4 lub 6, to ostatnią może być jedna z trzech pozostałych parzystych, a pozostałe 5 ustawiamy w środku dowolnie. Mamy tutaj 3*3*5! W sumie: 3*4*5!+3*3*5!=21*5!=21*120=2520

Piotr 10: dziękuję

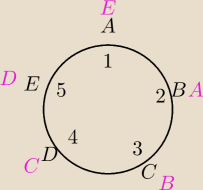
Mila: ZAdanie 1) 1,2,3,4,5 numery krzeseł A,B,C,D,E osoby a) Jeżeli bierzemy pod uwagę numery krzeseł na których siedzą te osoby, to te dwa ustawienia osób są różne. 5 osób można posadzić na 5! sposobów. b) jeżeli nie bierzemy pod wagę numerów krzeseł lecz tylko kto siedzi obok , to te dwa ustawienia są jednakowe.

5!
	=4!
5

możesz sobie dorysować następne przesunięcie, będzie ich 5

Mila: To ja już nie przeszkadzam.

Piotr 10: Mila mam pytanie Mam temat ''Wariacje'', i czy w tym temacie mogę wykorzystywać permutację?, np. Oblicz, ile róźnych liczb czterocyfrowych parzystych, w których wszystkie cyfry są różne, można utworzyć z cyfr 1,2,3,4,5,6,7 ? Ostatnia cyfra musi być postaci {2,4,6} Pierwsza cyfra na 6 sposobów... Druga cyfra 5 sposobów Trzecia cyfra 4 sposoby więc: 6*5*4*3=360

Piotr 10: A i mam jeszcze pytanie jedne jeśli z tym zadaniem(chodzi mi o okrągły stół) podałbym tylko jedną odpowiedź 5!=120 to był dostał maksymalną liczbę punktów czy nie ?

Saizou : oczywiście że można wykorzystać permutacje i wynik też dobry (ja nie widzę błędu)

Piotr 10: Ile jest wszystkich liczb pięciocyfrowych nieparzystych? ostatnia cyfra jest w postaci {1;3;5;7;9} 5 sposobów pierwsza druga trzecia i czwarta 9 sposobów 9⁴*5=32805 i tu wynik nie zgadza mi się co robię źle ?

Saizou : 1− cyfra {1,2,3,..8,9} czyli 9 sp. 2− cyfra {0,1,2,...8,9} czyli 10 sp. 3− cyfra {0,1,2...8,9} czyli 10 sp. 4− cyfra {1,3,5,7,9} czyli 5 sp. 9*10*10*5

Piotr 10: Ok, o tym zerze zapomniałem, wynik się zgadza dzięki

Saizou : zresztą jak nie byłeś tego pewien to mogłeś to zrobić z ciągów

Piotr 10: A faktycznie, ale wolę tą kombinatorykę trochę ogarnąć, bo średnio ogarniam

Saizou : tę kombinatorykę ale na maturze lepiej korzystać z bardziej pewnego źródła ale też trzeba umieć kombinatorykę

Piotr 10: Ja dyslektyk haha Wg mnie najgorszy to dział jest

Saizou : to co kilkanaście lat temu nie była wszelakiego rodzaju dys−.... i wszyscy, który chcieli, dawali jakoś radę

Piotr 10: No ale napisać ''tą'' a nie ''tę'' to chyba nie jakiś duży błąd. Jeżeli ktoś napisze np. ''bende'', ''rzycie'' to można dopiero to uznać za duży błąd. A w sumie to ja się nie znam na takich sprawach

Saizou : Twoje przykłady to raczej błędu ortograficzne, a tą książkę to przykład błędu językowego, bo to haczy o deklinację zaimka wskazującego to

Piotr 10: Spoko, ''deklinacja'' . Mi to słowo się kojarzy jedynie z fizyką ; )

Saizou : *błędy (literówka, często mi się zdarzają gdy piszę na komputerze)

Saizou : wolę określenie zboczenie magnetyczne

Piotr 10: Haha . Idź z tym magnetyzmem, nie lubię tego działu

Saizou : a ja całej fizyki, ale to szkopuł