Monotoniczność funkcji (pochodne)
matma!matma: Witam, mam takie zadanko:
Zbadaj jak się zachowuje ta funkcja: t
3 − 2t + 1
Nie jestem pewien ale przypuszczam, że chodzi o monotoniczność tej funkcji.
Zrobiłem to w ten sposób:
| | 1 | |
f(x)' = (t3 − 2t + 1)' = 3t2 − 2 = 6t −2 = 6(t − |
| ) |
| | 3 | |
Potrzebuję jakiś podowiedzi co z tym zrobić oraz czy to jest poprawnie.
Z góry dzięki
5 lis 00:08
Bizon:
ciekawe −

5 lis 00:18
matma!matma: co ciekawego tam dostrzegłeś? xD
5 lis 00:25
Godzio:
3t
2 − 2 = 6t − 2
Dla mnie to jest ciekawe

5 lis 00:26
Bizon:
f'(t)=3t2−2 .... to co napisałeś dalej to już "twórczość"
Ale można to bez pochodnych
t3−2t+1=(t−1)(t2+t−1)=(t−1)(t−...)(t+...) .... i wykres
5 lis 00:26
matma!matma: ok już widzę swój błąd

czyli do momentu 3t
2−2 jest w porządku?
moge z tego deltę policzyć czy musze to zrobić tak jak Bizon napisał?
5 lis 00:28
asdf:
t3 − 2t + 1 = t(t2−2) + 1 = t(t−√2)(t+√2) + 1, ale taka postac Ci nic nie da.
Policz:
f'(x) − aby dowiedzieć się o monotoniczności
f''(x) − aby znać wklęsłość/wypukłość tej funkcji
Jak Ci jeszcze czegoś do szczęścia brakuje to policz przecięcie się z osią OY. Dla
dokładniejszego naszkicowania funkcji dobrze jest mieć też ich asymptoty.
5 lis 00:29
matma!matma: @asdf
mógłbyś pokazać jak f'(x) z tego policzyć?
5 lis 00:31
Bizon:
... przecież da się to rozpisać ...−

5 lis 00:37
Bizon:
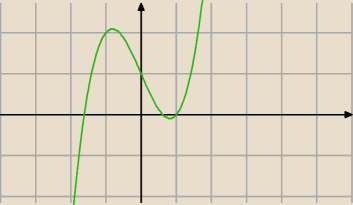
5 lis 00:51
matma!matma: Bizon mógłbyś rozpisać to ?
co po tym (t−1)(t2+t−1) zrobiłeś?
5 lis 00:59
Bizon:
... policz Δ i dalej rozpisz
5 lis 01:02
matma!matma:
i co teraz?

5 lis 01:07
Bizon:
... masz pierwiastki ....rysujesz wykres ...
5 lis 01:10
Bizon:
ale aby znaleźć ekstrema i tak musisz "zerować" pochodną
5 lis 01:13
matma!matma: aaa faktycznie teraz już to widzę, dzięki wielkie za pomoc i cierpliwość

5 lis 01:13
Bizon:
−

5 lis 01:14
asdf:
ale babola walnalem...nie f'(x) tylko f'(t)..
f'(t) = 3t2 − 2
f''(t) = 6t
5 lis 01:45


 czyli do momentu 3t2−2 jest w porządku?
moge z tego deltę policzyć czy musze to zrobić tak jak Bizon napisał?
czyli do momentu 3t2−2 jest w porządku?
moge z tego deltę policzyć czy musze to zrobić tak jak Bizon napisał?




